*) Имеется 10 уравнений относительно шести неизвестных; см. сноску 1 на стр. 474.

2) Таким образом, Wm имеет 7 элементов.

3) По терминологии теории чисел, отождествляются числа, сравнимые по модулю 7.

Применим это к множествам из Wm, перечисленным в (S3). В частности, мы получим

Щ + и>э + Щ > w2 + Щ + Щ, W2 + з + Щ > и\ + W5 + Wq, Щ + k + w6 > 2 + 3 + Щ 2 + 5 + 6 > 1 + 3 + Щ-

Сложив эти четыре неравенства, мы получим

2(w1 + W2 + W3 + W + W5+Wq) >2(Wi + W2 + W3 + W + W5 + W6),

т. е. противоречие.

Уравнениями (50:8) из пп. 50.4.3, 50.6.2, которые определяют главное простое решение, будут уравнения

f (Е3): xi + x2 + xb = 6, где 6 = 3, 4, 5, 6; (E z): xt + xa + Zb = 6, где а==3, 4; 6 = 5, 6. 3/* j (Eg): а?2 + р + = 6, где р = 3, д = 4 или р = 5, д = 6;

[ (ElY): х3 + х + х5 + х6 = 6.

Эти уравнения (Е3) неразрешимы Действительно, (El) показывает, что х3 = #4 и х5 = х6. Следовательно, (Ez ) дает х2 + 2#3 = 6, х2 + 2#5 = = 6; следовательно, х3 = х5 и поэтому х3 = xk = х5 = х6. Далее, (Ету) дает Ах3 = 6 и х3 = 3/2, в то время как (E z) и (Е3 ) дают 4 + 3 = 6 и #2 + 3 = 6, т. е. xi = #2 = 3. Наконец, из (Е3) мы получаем 3 + 3 + 3

+ у = 6 - противоречие.

Что касается интерпретации этой неразрешимости, то здесь по существу уместны те же комментарии, что и приведенные к соответствующему месту во втором замечании.

53.2.6. Шестое. Мы уже упоминали различие между принципом однородного взвешенного большинства и существованием главного простого решения, как обсуждалось в п. 50.8.2. Это было сделано в четвертом замечании, где был приведен пример для случая = в (50:21). Мы дадим теперь пример для случая > в (50:21).

Так как мы нашли, что для п 5 все простые игры являются однородными взвешенными мажоритарными играми, мы должны предполагать, что п 6. Мы не знаем, существует ли искомый пример для п = 6; в том примере, который мы приведем, п = 7.

Положим п = 7. Определим W как систему всех тех множеств S ( /= (1, . . ., 7)), которые содержат какое-нибудь из следующих семи трехэлементных множеств 2)

(S,) : (1, 2, 4), (2, 3, 5), (3, 4, 6), (4, 5, 7), (5, 6, 1), (6, 7, 2), (7, 1, 3).

Принцип, на котором основано это определение, может быть проиллюстрирован различными способами.

Вот один из них. Семь множеств (£4) получаются из первого (1, 2, 4) циклической перестановкой, т. е. увеличением номера каждого из своих элементов на любое из чисел 0, 1, 2, 3, 4, 5, 6, считая при этом, что числа 8, 9, 10, 11, 12, 13 тождественны соответственно числам 1, 2, 3, 4, 5, 6 3).

Другими словами, они получены из множества точек, помеченных крестиками на рис. 68, любым из семи поворотов, которые переводят эту фигуру в себя.

Другая иллюстрация. На рис. 69 изображена конфигурация игроков 1, . . ., 7, на которой можно непосредственно указать семь множеств из (54). Они указываются шестью прямыми линиями и окружностью 1).

Проверка того, что W удовлетворяет условиям (49:W*), нетрудна, но мы предпочитаем предоставить ее читателю, если он интересуется этим видом комбинаторики. Wm состоит, очевидно, из семи множеств (54)..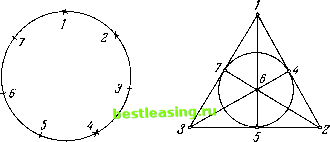

Рис. 68. Рис. 69.

Легко показать, что это не есть взвешенная мажоритарная игра-Мы опустим соответствующее рассуждение.

С другой стороны, уравнения (50:8) из пп. 50.4.3, 50.6.2 (с U = Wm)r которые определяют главное простое решение, таковы:

(2?4): ха-\- хь + хс = 7, где (а, Ь, с) пробегают 7 множеств (£4).

Эти уравнения, очевидно, имеют решение xt = . .. = хт = 7/32).

Мы можем теперь установить, что в (50:21) из п. 50.8.2 имеет место* знак >. Действительно,

2*1=у>14 = 2и.

Так же как и игры, которые обсуждались во втором, третьем и пятом замечаниях, эта игра соответствует организационному принципу, который заслуживает более пристального изучения. В этой игре каждое множество* из Wm, т. е. решающая выигрывающая коалиция, всегда составляет меньшинство (все они - трехэлементные множества). Тем не менее никакой игрок не имеет никаких преимуществ перед остальными. Рис. 68* и его рассмотрение показывают, что любая циклическая перестановка игроков 1, . . ., 7, т. е. любой поворот круга на рис. 68, оставляет структуру игры неизменной. Любой игрок может бьт? переведен этим способом на место любого другого игрока 3). Таким образом, структура этой игры

!) Читатель, который знаком с проективной геометрией заметит, что рис. 69 есть изображение так называемой 7-точечной плоской геометрии. Семь искомых множеств суть ее прямые линии, каждая из которых содержит по три точки, и окружность, обладающая тем же свойством.

2) Легко видеть, что это решение единственное.

3) Тем не менее эта игра не является безобидной в смысле п. 28.2.1, так как, например, два трехэлементных множества (1, 2, 4) и (1, 3, 4) действуют различно. Первое из этих множеств принадлежит W, а второе принадлежит L. (Так, в редуцированной форме игры, с у = 1, значение v {S) для первого множества равно 4, а для второго* равно - 3.)

г) Которые могут быть заданы правилами игры.

2) В этой игре нет никаких существенных связей между какими-либо игроками. Любых двух игроков можно перевести в любых двух других игроков соответствующей перестановкой (всех игроков 1, . . ., 7), относительно которой игра инвариантна.

определяется не индивидуальными свойствами игроков *) (как мы видим, все они в равном положении), а отношениями между игроками. Именно* взаимопонимание, достигаемое между тремя игроками, которые связаны в (£4) 2)> решает вопрос о победе или поражении.

§ 54. НАХОЖДЕНИЕ ВСЕХ РЕШЕНИЙ В СООТВЕТСТВУЮЩИХ ИГРАХ

54.1. Основания для рассмотрения в простых играх решений, отличных от главного решения

54.1.1. До сих пор при исследовании простых игр наше внимание было сосредоточено в основном на решениях специального типа, рассматривавшихся в пп. 50.5.1-50.7.2, и особенно на главном простом решении из п. 50.8.1. На основании изученного в предыдущих параграфах, особенно на основании примеров из п. 53.2, такой подход не представляется оправданным в равной мере для всех аспектов нашей задачи.

Прежде всего, мы видели, что нельзя ожидать, чтобы все простые игры имели решения указанного типа. Уже при п = 6 появляется обилие новых возможностей. Это знаменательно, так как 6 есть крупное число с комбинаторной точки зрения, но малое с точки зрения социальной организации.

Далее, даже когда эти решения существуют, фактически даже для случая однородных взвешенных мажоритарных игр, они не описывают полностью всего положения вещей. Для наиболее примитивного представителя такого класса, для существенной игры трех лиц, обозначаемой, как мы знаем, через [1, 1, 1], существует много решений. А рассмотрения в § 33 показывают, что все они важны для понимания характерных особенностей и выводов нашей теории - фактически некоторые основные интерпретации были получены впервые именно на этом пути.

54.1.2. Следовательно, важно уметь находить все решения простой игры и, пока мы не можем этого осуществить для всех простых игр, сделать это для возможно большего их числа. В частности, это должно быть сделано хотя бы для одной простой игры при каждом значении п. Эти результаты дали бы некоторые сведения о структурных возможностях и принципах классификации р<ешений для случая п участников.

Конечно, было бы в равной степени желательно получить такие сведения не только для простых игр. Однако простые игры обладают явным преимуществом перед всеми другими, когда решения нужно находить систематически. Именно, для простых игр так называемые предварительные условия из п. 30.1.1 не вызывают трудностей (см. п. 31.1.2), так как в этом случае каждое множество S или заведомо необходимо, или заведомо не необходимо (см. п. 49.7).

Ясно также, что подобные результаты дали бы сведения только относительно нескольких изолированных случаев. Тем не менее они охватили бы все п, т. е. позволили бы изменять п произвольно. Это может привести к важным интуитивным представлениям.