Заметим, что

(I) g(u0) = a0;

(II) #Ы = Ро.

А:Н) Это отображение w]->g(w) имеет следующие свойства:

(Г) оно монотонно; (1Г) для 0<р<1 и ю\фщ

((1-Р)о+М = (1-Р) ао+РгИ;

(ИГ) для 0<р<1 и и;фи0

8 ((1 -Р) *>о + Р) = (1 -Р) Ро + Ps И-

А:1) Отображение всех w из сегмента u0wu0 на любое мно-

жество чисел, обладающее свойством (I), (II) и либо (1Г). либо (ИГ), совпадает с отображением из (A:G).

Доказательство. Используя соответствие между функциями

gt (w) = (Ро - оо) /i (w) + а0,

или, что то же самое

Эо- о

(для /i(w;), gi(w), а также для /(и;), g(w)), мы видим, что утверждения (A:G) -(А:1) переходят в (A:D) - (A:F). Следовательно, (A:G) - (A:I) следуют из (A:D) - (A:F).

A:J) Беря (I) и (И) из (A:G), мы получаем, что уравнение

(щ u <С v и0), где u = u0 и ифщ, эквивалентно (IP) из (А:Н) и с 1£=ту0, у = у0 эквивалентно (ПГ) из (А:Н).

Доказательство. (1Г). Подставим u0, w, р вместо и, у, р. (ИГ). Подставим ш, 1 - Р вместо и, v, р.

А.2.3. В (A:G) - (А:1) отображение интервала полезностей щ w и0 *на числовой интервал а0 а ро было дано в удобной форме, заключающей в себе соответствующее свойство единственности. Теперь мы приступим к согласованию отображений

ф\К) Рассмотрим gjjjj;So и о* для которого u0w0u0. Положим

Тогда .?2j;2j() совпадает с g \Z°n(w) в области и00 (если и>ъфщ, т. е. если и0О0) и g\(w) совпадает с gl°0\l°0 в области WqwUq (если ш0фи0, т. е. если w0<C.v0).

Доказательство. Для gZX (Функция ggS.Sj И обладает свойствами (I), (1Г) (из (A:G) и (А:Н)) для а0, 7о, u0f w0, так как они те же, что ц для а0, Ро, Щ, Щ (они содержат лишь нижние границы а0, и0). Эта функция обладает также и свойством (II) (из (A:G)) для оь0, 7о, Щ, Щ,

потому что gZ\vl [щ) = Уо- Значит, из (А:1) следует, что gl°0]°0 удовлетворяет внутри Uq-wVo условию единственности gul\w0*

Для gZ°o,v°o- Функция guoJo обладает свойствами (II), (ПГ) (из (A:G), (А:Н)) для уо, Ро> Щ, v0, так как они те же, что и для а0, р0, w0, v0 (они содержат лишь верхние границы р0, v0). Эта функция также удовлетворяет (I) (из (A:G)) для y0i р0, wo, так как gl°0\%°0 (w0) = 70. Значит, из (А:1> следует, что gu00\v°0 Для w0 5g w v0 удовлетворяет условиям, определяющим единственную gXo,*o-

(A:L) Рассмотрим gullvl и щ, vu для которых щ 5g щ < vt г;0.

Положим оы = g2\v0 Ы и р4 = gZ\Z fa). Тогда g%X (w) сов-

падает с gu\\ v{ (w) в области изменения последней функции щ

Доказательство. Применим сначала (А:К) к gul\ll и к gu0\vi (т. е. с щ, vQ, а0, р0, vu $t соответственно в качестве щ, v0, а0, р0, w0, у0;.. заметим, что pf = gu°0\ %°0(vt)). Это показывает, что gu00\v00 {w) в области щ =\ w =1 i совпадает с guo,5l (w). Применим затем (А:К) к g2J;5i и к йь(£ (т. е. с и0у Ui, а0, рь м4 соответственно в качестве щ, v0, а0, р0, w0, у0;. заметим, что at = gSJJ; %°0 Мы получим, что gl°0\%°0 (w), а сле-

довательно, и gZ00\%°0(w), в области iiiwgvi совпадает с gullvl (и>).

(A:L) следует объединить со второй линией рассуждений. Здесь мы также предположим, что выбраны и* и v*y для которых и* <z;*; мы будем считать их фиксированными до тех пор, пока не перейдем, к (A:V) и (A:W).

Теперь докажем следующее:

(А:М) Если и* <iv* 5g v0, то существует единственная функция;

О И для К0Т°Р°Й

Доказательство. Построим / (w) = fUo, v0 iw) из (A:D). Так-как и* < и*, должно быть / (и*) < / (г;*). Для переменных а0 и р0 (A:G> дает gZ\l°0 (w) = (ро - a0) / (w) + a0. Следовательно, условия (I) и (II> означают, что (р0 - а0) / (и*) + а0 = О, (р0 - а0) / (v*) + а0 = 1, и эти два уравнения определяют единственные а0 и р0 х). Итак, искомая,

функция gu°0\ vl (w>) существует и единственна.

(A:N) Если щ v0 и* < г;* vt i;0t то йио> *0 (w) совпаДаег

с иь ui (w) в области ii fg w -\ V\.

Доказательство. Положим a4 = fewo, г?0 (wi) и р4 = hUOt vo (г). Тогда, по (A:L), hU(it vo (w) совпадает с g*\\ v[ (и?) в ее области щ <; w z. Применение этого к ш = и* и = дает нам §J (w) = feUo, vo (M*) = = 0 и Й1;51 (v*) -Ko.vo (*>*) = 1- Значит, по (A:M) должно быть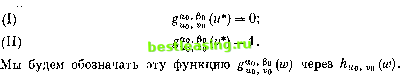

i) Именно,

Po =

1-/(ц*)

/( *)-/( *)

/( )-/( )

gu\\ v\ (w) - hui, V! (w)- Следовательно, hUQiVQ(w) совпадает с функцией huu vt (w) в ее области щ w vt.

Теперь мы можем установить желаемый факт: все hUOfVO (w) совпадают с одной и той же функцией. Конкретно, мы докажем следующее:

(А:0) Пусть дано произвольное w, тогда можно найти такие щ и v0r

что Uq и* <С v* fg v0 и щ 5g w v0. Для всех таких щ, v0. функция hUQfV0 (w) имеет одно и то же значение. Таким образом, ио, то (w) зависит только от w. Эту величину мы будем обозначать поэтому через h (w).

Доказательство. Существование щ, v0. Экстремумы и0 = = min (u*, w) и v0 = max (у*, w), очевидно, обладают требуемыми свойствами.

Переходим к доказательству того, что hUOiVO (w) зависит только от w. Выберем для этого две пары щ, v0 и и0, v0, для которых щ и* < v*

v0, щ g w g v0 и и0 -\ и* <Z v* v0, щ w g г/. Положим = = max (и0, щ) и Vi = min (v0, v0). Тогда u0 щ и* <. v* Vi = v0r щ w Vi и u0 щ и* <C v* Vi v0, щ fg w g i. Теперь, применяя дважды (A:N) (сначала с w0, v0, щ, vi4 w, а затем с щ, v0, uiy Vi, w), мы получим

Ко, vo И = Klt V! И И AuJ> rj (и?) = feUl> Vl (w).

Следовательно,

что и требовалось доказать.

А.2.4. Функция h(w) из (А:0) определена для всех полезностей и принимает числовые значения. Мы можем теперь без особого труда показать, что она обладает всеми требуемыми свойствами.

Легче всего это сделать с помощью двух вспомогательных лемм.

(А:Р) Пусть даны любые и, v, для которых и << v; тогда существуют

такие щ, v0, что щ ;rg и* < v* 5g v0, и0 и < v :=g v0.

Доказательство. Положим щ = min (и*, и) я v0 = = max (у*, у).

(A:Q) Пусть даны любые и, v, причем и < v. Положим h (и) = а,

h (v) = р. Тогда а<р и функция h ( w) в области и w v совпадает с gu\ S (w).

Доказательство. Выберем щ, v0, как это указано в (А:Р). По (А:М) функция hUQt VQ (w) принадлежит к числу gu°0\ щ (и>) с соответствующими а0 и р0. По (А:0) h (w) совпадает с hUQiV0 (w), т. е. с gu°0]vo {w) в области щ :fg w 5g v0. Для w = и и w = v это дает нам соответственно gu0\ щ (и) = h (и) = а] и Й2: SS =h(v) = р. Так как функция eu°Q,vl (w) монотонна, должно быть сс <С р. Далее, по (A:L) (с щ, v0, os0, ро, и, v, а, р соответственно в качестве щ, v0, сс0, ро o&i, pi) функция

gul\ v°0 (u>) совпадает с функцией gu\ v (w) в области и w v. Следовательно, то же самое верно и для h (w).

После этой подготовки мы установим интересующие нас свойства h (w)

(A:R) Отображение w->h(w) всех w на множество чисел обладает

следующими свойствами:

(I) М *) = 0;