

 |
 |

|
Промышленный лизинг
Методички
8.2, Множества, их свойства и их графическое представление 8.2.1. Множеством называется произвольная совокупность объектов (на природу и количество которых не накладывается абсолютно никаких ограничений), называемых элементами рассматриваемого множества. Элементы образуют и определяют множество как таковое; никакого упорядочения или отношений иного рода между ними не предполагается. Иначе говоря, если два множества А и В таковы, что любой элемент А является также элементом В и наоборот, то эти множества тождественны во всех отношениях, т. е. А = В. Тот факт, что а является элементом множества А у мы выражаем также, говоря, что а принадлежит А г). Нас будут интересовать главным образом (хотя и не всегда) только конечные множества, т. е. множества, состоящие из конечного числа элементов. Пусть даны произвольные объекты а, 3, у, . . .; множество, элементами которого они являются, будет обозначаться через (а, (3, 7, . . .). Будет также удобно ввести множество, которое вовсе не содержит элементов,- пустое множество 2). Мы будем обозначать пустое множество через 0. В частности, мы можем образовывать множества, состоящие в точности из одного элемента,- одноэлементные множества. Одноэлементное множество (а) и его единственный элемент а представляют собой вовсе не одно и то же и поэтому никогда не должны смешиваться 3). Подчеркнем еще раз, что элементами множества могут быть любые объекты. Разумеется, мы ограничимся математическими объектами. Эти элементы вполне могут быть, например, множествами, что приведет к рассмотрению множеств множеств и т. д. Последние нередко называются, например, системами или классами множеств, хотя это и не обязательно. 8.2.2. Перечислим основные понятия и операции, связанные с множествами. (8:А:а) А является подмножеством В (В является надмножеством А), если любой элемент А является также элементом В. Символически это записывается в виде А В или В з А. А является собственным подмножеством В, а В - собственным надмножеством Ау если сказанное выше верно, но В содержит элементы, не являющиеся элементами А. В символах: А а В или В zd А. Мы видим, что если А является подмножеством В ж В является подмножеством А, то А =В. (Это представляет собой переформулировку принципа, высказанного в начален. 8.2.1.) Отметим еще, что А является х) Математическая литература по теории множеств весьма обширна. Мы не будем пользоваться ею в пределах, выходящих за рамки изложенного в тексте. Заинтересованный читатель найдет больше сведений по теории множеств в хорошем вводном курсе: A. Fraenkel, Einleitung in die Mengenlehre, Berlin, 1928, а также в сжатой и технически превосходной книге F. Hausdorff, Mengenlehre, 2nd Edit, Leipzig, 1927 (рус. пер. Ф. Хаусдорф, Теория множеств, ОНТИ, 1937). 2) Если два множества А и В оба не содержат элементов, то мы можем сказать, что они содержат одни и те же элементы. Следовательно, в силу сказанного выше А = = В. Иначе говоря, существует только одно пустое множество. Это рассуждение может показаться странным, но тем не менее оно безупречно. 3) В нерсоторых разделах математики (а) и а можно отождествить. Это время от времени и делается, однако такую практику следует считать нездоровой. В общем случае это, конечно, недопустимо. Пусть, например, а представляет собой нечто, решительно не являющееся одноэлементным множеством, например, а есть двухэлементное множество (Р, у) или пустое множество 0. Тогда (а) и а следует различать, так как (а) является одноэлементным множеством, а а им не является. собственным подмножеством В в том и только в том случае, когда А является подмножеством В и не имеет места равенство А = В. (8:А:Ь) Суммой или объединением двух множеств А и В называется множество всех элементов А вместе со всеми элементами В. Объединение А и В будет обозначаться через A (J В. Аналогично образуются объединения более чем двух множеств 1). (8:А:с) Произведением или пересечением двух множеств А и В называется множество всех общих элементов А и В. Пересечение А и В будет обозначаться через A f В. Аналогично образуются пересечения более чем двух множеств 1). (8:A:d) Разностью двух множеств А и В называется множество всех тех элементов А, которые не принадлежат В. Разность А и В будет обозначаться через А - В *). (8:А:е) Если В является подмножеством А, то мы будем называть разность А - В дополнением В в А. Иногда будет настолько очевидным, какое множество А имеется в виду, что мы будем писать просто -В и говорить просто о дополнении множества В без всяких дальнейших уточнений. (8:A:f) Два множества А и В называются непересекающимися (дизъюнктными), если они не имеют общих элементов, т. е. если А (\В = 0. (8: A:g) Система (множество) А множеств называется системой попарно непересекающихся множеств, если все пары различных элементов системы Л представляют собой дизъюнктные множества, т. е. для А, В £<Л из А ф В следует А [\ В = 0. 8.2.3. Здесь могут оказаться полезными некоторые графические иллюстрации. Мы будем обозначать объекты, являющиеся в этих рассмотрениях элементами множеств, точками (рис. 1). Множество будет обозначаться путем обведения принадлежащих ему точек (элементов), причем обозначающий множество символ будет писаться в разрыве обводящей линии в одном или в Рис. 1. нескольких местах. Изображенные на рис. 1 множества А и С являются непересекающимися, а множества А и В таковыми не являются. С помощью этого приема можно проиллюстрировать также понятия объединений, пересечений и разности множеств (рис. 2). На этом рисунке х) Эта терминология (суммы, произведения, разности) является традиционной. Она основана на некоторых алгебраических аналогиях, которые мы здесь использовать не будем. В действительности алгебра этих операций \J, f известная под названием булевой алгебры, имеет большой самостоятельный интерес. См., например, А. Т а г s k i, Introduction to logic, New York, 1941, а также G. В i r kh о f f, Lattice theory, New York, 1940 (русский перевод: Г. Б и p к г о ф, Теория структур, М., ИЛ, 1952). Последняя книга представляет большой интерес для понимания современного абстрактного метода. Гл. VI посвящена булевым алгебрам; там же указана дальнейшая литература.  А не является подмножеством В, равно как и В не является подмножеством А; следовательно, ни разность А -В, ни разность В -А не являются дополнением одного из этих множеств до другого. На следующем рисунке, однако, В является подмножеством А, так что А - В является дополнением В в А (рис. 3). 8.3. Разбиения, их свойства и их графическое представление 8.3.1. Пусть дано множество Q и система множеств А. Мы будем говорить, что Jh является -разбиением в Q, если оно удовлетворяет следующим двум требованиям: (8:В:а) Любой элемент А системы Jh является непустым подмножеством множества Q. (8:В:Ь) Jh представляет собой систему попарно непересекающихся множеств. Это понятие также породило обширную литературу *). Если даны два разбиения Jh и 98, то мы будем говорить, что Л является подразбиением 98, если они удовлетворяют следующему условию: (8:В:с) Любой элемент А разбиения Jh является подмножеством некоторого элемента В разбиения 98 2). Отметим, что если Jh является подразбиением 98 и 98 является подразбиением Jh, то Jh = 98 3). Сформулируем теперь следующее определение. х) См. цитированную в сноске на стр. 88 книгу Г. Биркгофа. Наши требования (8:В:а), (8:В:Ь) не совпадают дословно с общепринятыми. Именно в (8:В:а) иногда не требуется, чтобы элементы А системы Jh были непустыми. Действительно, нам придется сделать одно исключение в п. 9.1.3 (см. сноску 1 на стр. 95). В условии (8:В:Ь) обычно требуется, чтобы объединение всех элементов Jh было равно множеству Q. Для наших целей будет более удобным это требование опустить. 2) Так как Jh и 99 также представляют собой множества, уместно сравнить отношение быть подмножеством (применительно к Jh и 99) с отношением быть подразбиением . Легко видеть, что если Jh является подмножеством 9В, то Jh является и подразбиением 9В, но обратное, вообще говоря, неверно. 3) Доказательство. Рассмотрим некоторый элемент i из i. Он должен быть подмножеством некоторого элемента В из 9В, а В в свою очередь - подмножеством некоторого элемента At из Jh. Таким образом, А и А имеют общие элементы (именно все элементы непустого множества А) и тем самым не являются дизъюнктными. Так как оба они принадлежат разбиению Jk, отсюда следует А = At. Поэтому А является подмножеством В, а В - подмножеством А (= А). Следовательно, А = В, так что А принадлежит 38. Отсюда мы получаем, что Jh есть подмножество 9В (см. предыдущую сноску). Аналогично & является подмножеством Jh. Следовательно, Jh = 9В. 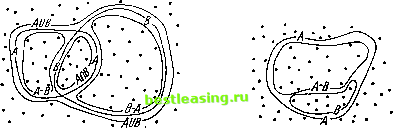 Рис. 2. Рис. 3. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 [ 21 ] 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 |