(8:B:d) Пусть даны два разбиения Л и 98. Образуем систему всех непустых пересечений A f В, где А пробегает все элементы Л, а В - элементы 98. Очевидно, мы снова получим разбиение, называемое суперпозицией Л и г).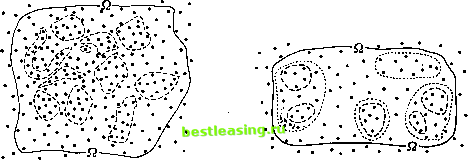

Рис. 4. Рис. 5,

Определим, наконец, описанные выше соотношения для двух разбиений Л и па данном множестве С.

(8:В:е) Л является подразбиением на множестве С, если любое А, принадлежащее Л и являющееся подмножеством С, является также подмножеством некоторого 5, которое принадлежит 98 и является подмножеством С.

(8:B:f) Л равно 98 на множестве С, если элементами Л и 98 являются одни и те же подмножества множества С.

Очевидно, сноска 3 со стр. 89 снова применима - с соответствующими изменениями. Кроме того, определенные сейчас понятия на множестве £2 совпадают с первоначальными понятиями.

8.3.2. Приведем снова некоторые графические иллюстрации в смысле п. 8.2.3.

Начнем с изображения разбиения. Мы не будем обозначать элементы разбиения, представляющие собой множества, буквами, а будем обводить каждое из них пунктиром (рис. 4).

Далее мы изобразим два разбиения Jb и 98 \ для различения их условимся изображать обводящие линии элементов Л длинным пунктиром, а элементов $ - коротким пунктиром. На рис. 5 Л является подразбиением 98. На следующем рис. 6 Л не является подразбиением 98 и 98 не является подразбиением Л. Предоставляем читателю определить суперпозицию Л и 98 на рис. 6.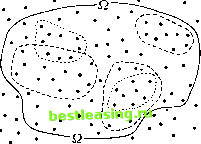

Рис. 6.

г) Легко показать, что суперпозиция разбиений Л и & является подразбиением как Л, так и J и что любое разбиение %, представляющее собой подразбиение как Л, так и оказывается также подразбиением их суперпозиции. Отсюда происходит и название. См. гл. I и II цитированной выше книги Г. Биркгофа.

Рис. 7. Рис. 8.

составляющих элементы разбиения, и не может быть использовано для изображения одновременно нескольких разбиений в Q, как это было проделано на рис. 6. Этот недостаток, однако, может быть устранен, если два разбиения А и 98 в Q соотносятся так, как на рис. 5, а именно если А является подразбиением 98. В этом случае мы снова можем представить Q точкой внизу, каждый элемент 98 - отрезком, идущим вверх от этой точки, как на рис. 7, а каждый элемент А - другим отрезком, идущим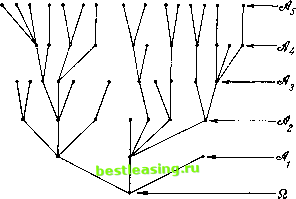

Рис. 9.

дальше вверх и начинающимся в верхнем конце того отрезка 98, который представляет элемент 98, подмножеством которого является этот элемент А. Мы можем таким образом представить два разбиения А и 98, изображенные на рис. 5 (см. рис. 8). Это представление опять-таки является менее наглядным, чем соответствующее ему изображение на рис. 5. Однако его простота позволяет продолжить его гораздо дальше, чем могут практически зайти картинки в духе рис. 4-6. Именно, мы можем изобразить при помощи этого приема последовательность разбиений А, . . . . . ., А, в которой каждое разбиение является подразбиением своего непосредственного предшественника. На рис. 9 изображен пример для [I = 5.

Конфигурации такого типа уже изучались в математике; они называются деревьями.

Другое, более схематичное описание разбиений можно получить, представляя множество Q одной точкой, а любой элемент разбиения, представляющий собой подмножество Q, отрезком, идущим из этой точки вверх. Тогда разбиение А (рис. 5) будет представлено гораздо более простым чертежом (рис. 7). Такое представление не указывает элементов,

8.4. Логическая интерпретация множеств и разбиений

8.4.1. Описанные в пп. 8.2.1, 8.3.2 понятия будут полезными в последующем рассмотрении игр в силу той логической интерпретации, которая может быть им приписана.

Начнем с интерпретации множеств.

Если Q представляет собой множество объектов любой природы, то любое мыслимое свойство, которым некоторые из этих объектов могут, а другие не могут обладать, можно полностью охарактеризовать указанием множества тех элементов й, которые этим свойством обладают. Иначе говоря, если два свойства соответствуют в этом смысле одному и тому же множеству (одному и тому же подмножеству Q), то этими двумя свойствами будут обладать одни и те же элементы Q. Сказанное означает, что эти свойства эквивалентны в Q в том смысле, как это понимается в логике.

Теперь уже не только свойства (элементов Q) находятся в этом простом соответствии с множествами (подмножествами Q), но и элементарные логические операции над этими свойствами оказываются находящимися в соответствии с теоретико-множественными операциями, рассмотренными нами в п. 8.2.2.

Так, дизъюнкция двух свойств, т. е. утверждение о том, что справедливо по крайней мере одно из них, соответствует, очевидно, образованию объединения их множеств - операции А [} В. Конъюнкция двух свойств, т. е. утверждение о том, что оба они справедливы, отвечает образованию пересечения соответствующих множеств - операции A f В. Наконец, отрицание некоторого свойства, т. е. утверждение противоположного, отвечает образованию дополнения соответствующего множества, операции -А х).

Вместо сопоставления подмножеств множества Q свойствам объектов из Q, как это было проделано выше, мы можем равным образом сопоставить их всем возможным объемам информации, относящимся к некоторому, в остальном неопределенному, элементу из Й. Действительно, любая такая информация сводится к утверждению о том, что этот неизвестный элемент из Q обладает определенным конкретным свойством. Эту информацию можно эквивалентным образом представить при помощи множества всех тех элементов из Q, которые этим свойством обладают; иначе говоря, при помощи множества, до которого данная информация сужает область возможного изменения этого неизвестного элемента из Q.

Отметим, в частности, что пустое множество 0 соответствует свойству, которое никогда не имеет места, т. е. абсурдной информации. Два непересекающихся множества отвечают двум несовместным свойствам, т. е. двум взаимно исключающим объемам информации.

8.4.2. Обратимся теперь к разбиениям.

Возвращаясь к определениям (8:В:а) и (8:В:Ь) из п. 8.3.1 и переформулируя их в нашей новой терминологии, мы видим, что разбиение представляет собой систему попарно взаимно исключающих объемов информации (относительно некоторого неизвестного элемента из Q), ни один из которых не является сам по себе абсурдным. Другими словами, разбиение является предварительным сообщением, которое говорит, сколько информации будет впоследствии дано по поводу некоторого (в остальном неизвестного) элемента из Q, т. е. до какой степени будет в дальнейшем сужена

*) По поводу связей теории множеств и формальной логики см., например, гл. VIII цитированной выше книги Г. Биркгофа.