Положим ai=zt - yi; тогда случай at = ... =ап = 0 исключается, так как

-* -> *

%Фу (см. предыдущие рассуждения). Положим также Ъ~ 2j aiUi- Таким

образом, равенство

(16:2:а*) Sc = b

->

определяет гиперплоскость, которой точка г/, очевидно, принадлежит. Далее, пусть

(16:2:Ь*) 2***.>ь

- полупространство, порожденное этой гиперплоскостью; тогда (16:4) ->

утверждает, что и принадлежит этому пролупространству.

Поскольку и - произвольный элемент из С, доказательство завершено.

Это алгебраическое доказательство можно провести также на геометрическом языке.

Сделаем это сначала для случая п = 2 (т. е. для плоскости). Ситуация

-> ->

изображена на рис. 19: z - точка из С, ближайшая к данной точке у;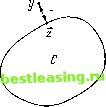

Гиперплоскость (16-3) Рис. 19. Рис. 20.

это значит, что расстояние z - у \ принимает на z свое минимальное

значение. Поскольку у и z фиксированы, а и-переменная точка (принадлежащая С), неравенство (16:3) определяет гиперплоскость и одно

из полупространств, порожденных ею. Легко проверить, что z принадле-

жит этой гиперплоскости и сама гиперплоскость состоит из точек и, для которых эти три точки образуют прямой угол (т. е. для которых

векторы z - у и и - z %ортогональны). Фактически это означает, что

2 (zt - Уг) (иг - zi) - 0- Очевидно, что все множество С должно лежать

на этой гиперплоскости или по ту сторону от нее, которая не содержит у. Если какая-либо точка и из С лежала бы на г/-стороне,#то нашлись бы точ-

ки из сегмента [z, и], лежащие ближе к г/, чем z. (См. рис. 20. Вычисления на страницах 161-162, в надлежащей интерпретации, именно это и показывают.) Поскольку С содержит зима, следовательно, и весь сегмент [z, и], это противоречит утверждению о том, что точка z является ближайшей точкой к у из точек множества С

§ 16] * ЛИНЕЙНОСТЬ и выпуклость 163

Переход от (16:3) к (16:4) соответствует параллельному переносу гиперплоскости I в положение II (параллельному, ибо коэффициенты

т = Zi - yt при ut, i = 1, . . ., п, не изменяются.) Теперь у принадлежит гиперплоскости, а С - порожденному ею полупространству (рис. 21).

Случай 72 = 3 можно наглядно представить себе сходным образом.

Такой геометрический способ рассуждений можно распространить и на произвольное п. Если читатель сможет убедить себя в том, что он обладает тг-мерной геометрической интуицией , то Предыдущие рассуждения могут быть восприняты как доказательство, верное в пространстве п измерений. Можно даже избежать и этого, рассуждая следующим способом. Каково бы ни было п, доказательство имеет дело одновременно только с тремя точками, а именно

с точками у, z, и. Через три точки всегда мож- Рис. 21.

но провести плоскость (двумерную). Если мы будем рассматривать только эту плоскость, то рис. 19-21 и связанные с ними рассуждения могут быть использованы без дополнительной интерпретации.

Как бы то ни было, приведенное выше чисто алгебраическое доказательство является абсолютно строгим. Мы привели геометрические аналогии главным образом в надежде, что* это облегчит понимание алгебраических выкладок, выполненных в ходе доказательства.

16.4. Теорема об альтернативах для матриц

16.4.1. Теорема (16:В) позволяет сделать очень важный для нашей дальнейшей работы вывод.

Мы начнем с рассмотрения прямоугольной матрицы в смысле п. 13.3.3 с п строками и т столбцами и элементами a(i, у). (См. рис. 11 в п. 13.3.3, где ф; х, у, t, s соответствуют нашим a, i, j, п, т.) Иными словами, a (i, у) является совершенно произвольной функцией двух переменных i -- = 1, . . ., п и у = 1, . . ., т. Построим некоторые векторы из Ьп.

Для каждого 7 = 1, . . ., т возьмем вектор хд = {х\, . . ., х3п} с х{=

= a (i, 7), а для каждого 1 = 1, . . ., п - координатный вектор 6==

= {6jJ (см. конец п. 16.1.3; мы здесь заменили / на Z). Применим теперь

->

теорему (16:В) из п. 16.3 в случае р = п-{-ткп-{-т векторам х1, ... . . ., хт, б1, . . ., бп (которые выступают в роли х1, . . ., xv). Положим

у = о.

Выпуклое множество С, натянутое на х1, . . ., хт, б1, . . ., бп, может содержать 0. Если это имеет место, то из (16:2:d) в п. 16.2.2 следует, что

(16:5) tO, tm0, sO, sn0,

(16:6) 2*>+Е*г = 1

j=l 1=1

(мы заменили tu ..., tp на tu .... tm, s4, sn). В покомпонентной записи это равносильна

Jjtja(h /)+ 2*-0.

j=i z=i

Второе слагаемое слева равно st, так что можно написать

(16:7) Sa(i, -5,.

Если бы имело место 2 tj 0, то были бы справедливы равенства f4 -

= ...=-0и, следовательно, из (16:7) вытекало бы, что s4 - . . . = 5Л=0.

Это, однако, противоречит (16:6). Следовательно, 2/>0- Заменим

равенство (16:7) его следствием

(16:8) 2а(£, j)tj0.

т i т

Положим теперь Xj= tjl 2 tj Для 7 = 1 Тогда мы получим 2 #7 = 1

j=l i=l

и (16:5) дает нам #42г0, #mi0. Следовательно,

(16:9) х = {хи . . ., л:т}6т,

и (16:8) приводит к условию

(16:10) J\a(i9j)xj0 для / = 1, п.

Рассмотрим, с другой стороны, случай, когда С не содержит 0. Теорема (16:В) из п. 16.3 позволяет нам сделать вывод о существо-

вании такой содержащей у гиперплоскости (см. (16:2:а) из п. 16.2.1), что множество С содержится в полупространстве, порожденном этой гиперплоскостью (см. (16:2:Ь) из п. 16.2.1). Обозначим эту гиперплоскость через

2 dtXi = ъ.

Поскольку 0 принадлежит ей, то 6 = 0. Таким образом, рассматриваемое полупространство имеет вид

(16:11) 2>0.

- -> - ->

Векторы х1, хт, б1, бп принадлежит этому полупространству.

При записи этого факта для 6* неравенство (16:11) принимает вид

2а*г>0, т. е. ai>0. Таким образом, мы получаем г=1

(16:12) а4>0, ап>0.