вероятным (т. е. он заменяет вероятность в 60% на достоверность). Это, однако, порождает некоторое заблуждение, будто этот процесс приводит к полной победе Шерлока

Холмса, тогда как шансы (т. е. значение партии), как мы уже видели, благоприятст-

-> ->

вуют Мориарти. Из нашего результата для g и к) вытекает, что Шерлок Холмс был уже с вероятностью 48% мертв, когда его поезд отошел от вокзала Виктории. См. в связи с этим высказывание в цитированной выше книге Моргенштерна (стр. 98) о том, что вся поездка была ненужной, поскольку проигрывающего можно определить с самого начала.

18.5. Рассмотрение несколько более сложных игр

18.5.1. Полученное в п. 17.8 общее решение игры двух лиц с нулевой суммой вводит определенные альтернативы и понятия, в частности наличия или отсутствия полной определенности, значения партии vr и множеств оптимальных стратегий Л, В. Для всех этих понятий мы получили в п. 18.2 достаточно простые явные характеристики и определения. Они оказались пригодными даже в п. 18.3 при переформулировке всех результатов.

Эта простота может привести даже к некоторым недоразумениям. Действительно, результаты в пп. 18.2 и 18.3 получены с помощью непосредственных и притом вполне элементарных вычислений. Комбинаторные критерии полной определенности (18.А), (18.С) в п. 18.3, по крайней мере в их окончательном виде, были также значительно более прямолинейными по сравнению с встречавшимися ранее. Это может вызвать сомнение в необходимости привлекать рассмотрения из п. 17.8 (и соответствующие результаты из п. 14.5 для случая полной определенности), особенно потому, что они основаны на математической теореме в п. 17.6, для которой был необходим анализ линейности и выпуклости в § 16. Если бы все это можно было заменить на рассуждения в стиле пп. 18.2, 18.3, то наши рассмотрения в §§ 16 и 17 были бы совершенно необоснованными х).

Но это не так. Как указывалось в конце п. 18.3, чрезвычайная простота процедур и результатов в пп. 18.2 и 18.3 является следствием того факта, что они приложимы только к очень простым играм двух лиц с нулевой суммой, именно к играм типа орлянки , для которых р4 = f52 = 2. По-видимому, для общего случая более абстрактные построения из §§ 16 и 17 пока представляются необходимыми.

Для того чтобы правильно понять взаимосвязь этих вещей, мы на нескольких примерах покажем, что для больших значений 3 утверждения из пп. 18.2, 18.3 уже не имеют места.

18.5.2. Для наших целей достаточно рассмотреть игры с р4 = р2 = 3. По существу они будут несколько напоминать игру в орлянку - большая общность получена только за счет введения третьей альтернативы.

Таким образом, оба игрока имеют альтернативы (т. е. значения для т1? т2) 1, 2, 3. Для читателя лучше всего подразумевать под выбором 1 решетку , под выбором 2 - герб и под выбором 3 что-нибудь вроде безымянный . Снова пытается угадать игрок 1. Если f одного из игроков безымянный , то не имеет значения, что у другого - герб или решетка ; существенно лишь одно: у другого тоже безымянный или же у него одна из первых двух возможностей.

Поэтому в данной игре матрица будет иметь вид, представленный в табл. 11.

*) Конечно, они не утратили бы строгости, но было бы совершенно необоснованным использование сложного математического аппарата для элементарной задачи.

Таблица 11

Четыре первых элемента матрицы (т. е. первые два элемента в первых двух строках) соответствуют уже знакомому примеру игры в орлянку (см. табл. 2). Два элемента, равные а, соответствуют случаю, когда игрок 1 выбирает безымянный и выбор игрока 2 не совпадает с выбором

игрока 1. Два элемента, равные у, соответствуют противоположной ситуации. Элемент, равный 3, соответствует случаю, когда оба игрока выбирают безымянный . Придавая соответствующие значения (положительное, отрицательное или нуль), мы можем каждой из этих ситуаций поставить в соответствие премию или штраф или же сделать ее безразличной.

Мы получим все эти примеры, когда они нам понадобятся, конкретизируя нашу схему, т. е. выбирая соответствующим образом указанные выше а, 3, у.

18.5.3. Наша задача состоит в том, чтобы показать, что ни один из результатов (18:А), (16:В), (18:С), вообще говоря, не верен.

По поводу (18:А). Этот критерий полной определенности относится к частному случаю р4 = р2 = 2. Для больших значений р1э р2 две диагонали даже не будут исчерпывать матрицы, и, следовательно, положение дел только на диагоналях не может быть такой же характеристикой, как это было выше.

По поводу (18:В). Приведем пример игры, которая не является вполне определенной, но в которой тем не менее существует оптимальная стратегия одного из игроков, являющаяся чистой (конечно,

для другого игрока это уже не так). Кроме Таблица 12

того, особенность этого примера состоит в том, что у одного из игроков имеется несколько оптимальных стратегий, в то время как у другого - только одна.

Возьмем для игры, описываемой табл. 11, а, Р, у из табл. 12. Здесь а > 0, 6 > 0. Для себя читатель определит, какие комбинации выбора безымянный соответствуют выигрышу или штрафу в указанном выше смысле.

Проанализируем эту игру, используя критерии из п. 17.8.

Для £ = {У2, У2, 0} всегда К (£ $ = 0, т. е. при этой стратегии игрок 1 не может ничего потерять. Следовательно, v 0. Для ц = 8s = {0, 0, 1} всег--у ->

да К (£, г) rgO1), так что при этой стратегии не может ничего потерять игрок 2. Следовательно, v fg 0. Таким образом, имеем

v = 0.

Поэтому £ является оптимальной стратегией в том и только том случае, когда К (£, г]) 0, а г] является оптимальной стратегией в том и только

*) Действительно, в данном случае К (£, г)) = - 6£3.

том случае, когда *) К (£, т]) rg 0. Легко видеть, что первое справедливо тогда и только тогда, когда

1 = 2 = j Нз = 0,

а второе -тогда и только тогда, когда

ЧТетбР 43 = 1-2%.

Таким образом, множество -4 оптимальных стратегий состоит ровно

из одного элемента, и этот элемент не является чистой стратегией. В то же

- ->

время множество В оптимальных стратегий г\ содержит бесконечно много

-> ->

стратегий, одна из которых является чистой, именно т] = б3 = {0, 0, 1}.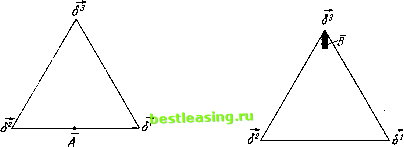

Рис. 22. Рис. 23.

Множества А и В можно представить графически, используя графическое представление по аналогии с рис. 16 (см. рис. 22, 23).

По поводу (18:С). Приведем пример вполне определенной игры, в которой никакие две строки, а также никакие два столбца не доминируют друг друга. Фактически мы сделаем даже несколько больше.

18.5.4. Предположим пока, что числа р1? р2 произвольны. Сущность доминирования строк и столбцов была рассмотрена в конце п. 18.3. Как было показано, это означает, что у одного из игроков имеется простой и непосредственный повод отказаться от одной из своих возможностей ради другой,- и это сужает возможности в направлении, приводящем в конечном счете к полной определенности.

В частности, если строка т[ доминируется строкой т. е. если (Ti т2) (1, т2) для всех т2, то игроку 1 можно не рассматривать выбор Tj, поскольку при любых обстоятельствах выбор %[ не хуже выбора т . Если столбец т2 доминирует столбец т2, т. е. если (тА, т2) е/Г (т15 т2) для всех т4, то игроку 2 можно не рассматривать выбор т2, поскольку при любых обстоятельствах выбор т[ для него не хуже выбора т2. (См. приведенное выше, в частности сноску 2 на стр. 197. Это рассмотрение, конечно, является чисто эвристическим, см. замечание на стр. 204.)

Теперь мы можем использовать более общее положение. Если строка % х (т. е. чистая стратегия игрока 1, соответствующая строке т[) доминируется линейной комбинацией оставшихся строк т[ Ф %\ (т. е. смешан-->

ной стратегией £, в которой компонента £т* ==0), то правдоподобно

х) Читателю предоставляется дать простую словесную интерпретацию этих утверждений.