19.9. Детальный анализ решения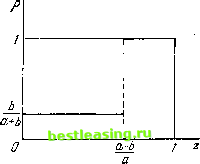

Рис. 24>

19.9.1. Полученные в п. 19.8 результаты показывают, что для рассматриваемой формы покера существует одна и только одна оптимальная стратегия х). Она описывается формулами (19:21), (19:12), (19:13) из п. 19.8. Мы изобразили эту стратегию графически, что облегчит последующее ее обсуждение. (См. рис. 24. Фактические пропорции этого чертежа соответствуют отношению alb ~ 3.)

Сплошная линия описывает кривую р = pf. Таким образом, высота этой линии над линией р = 0 равна вероятности высокой ставки pf; превышение линии р = 1 над сплошной линией равно вероятности низкой ставки (с обязательным последующим пасованием): pf = 1 - pf.

19.9.2. Формулы (19:9:а*), (19:9:Ь*), (19:9:с*) из п. 19.7 позволяют вычислить теперь коэффициенты у). Вместо формул мы дадим графическую интерпретацию, предоставляя читателю элементарную проверку. (См. рис. 25. Фактические пропорции остались здесь теми же, что и

на рис. 24, т. е. alb ~ 3.) Сплошная линия соответствует кривой у = Yf, точечная линия - кривой у = у*, а пунктирная?линия - кривой у = у На рисунке видно, что сплошная и пунктирная линии (т. е. yl и у*) совпадают на интервале 0 z (а - \р)1а, а линии точечная и пунктирная (т. е. у\ и у\) - на интервале (а - Ъ)1а z 1. Каждая из трех кривых составлена из двух отрезков, с общим концом в точке

z = а-- . Фактические значения

величин у) в критических точках z = О, (а - Ь)/а, 1 можно увидеть на рисунке 2).

19.9.3. Сравнение рис. 24 и 25 показывает, что наша стратегия дей-Рис. 25. ствительно является оптимальной,

т. е. что она удовлетворяет условию (19:В) из п. 19.7. В самом деле, на интервале 0 g z fg (а - Ь)/а, где выполняются оба неравенства pf =0, pf Ф 0, как кривая у\, так и

х) Фактически мы доказали только следующее утверждение. Никакая стратегия, отличная от стратегии, определенной в п. 19.8, не может быть оптимальной. То, что эта стратегия на самом деле является оптимальной, можно было бы заключить из существования (по крайней мере) одной оптимальной стратегии, хотя наш переход к непрерывному случаю и может вызвать некоторое сомнение. Далее мы убедимся в том, что рассматриваемая нами стратегия является оптимальной, т. е. что она удовлетворяет условию (19:В) из п. 19.7.

2) Проверку этих результатов мы предоставляем читателю.

кривая yl являются нижними, т. е. их ординаты равны min yj. На интервале

(а - Ъ)1а < z rg 1, где только pf Ф 0, только одна кривая у\ оказывается

нижней, т. е. ее ординаты равны min у]. (Поведение у\ несущественно,

поскольку всегда pf = 0.)

Формула (19:7*) из п. 19.7 позволяет вычислить также значение партии К. Очевидно, К = 0. Именно этого значения и следовало ожидать поскольку игра симметрична.

19.10. Интерпретация решения

19.10.1. Хотя результаты из пп. 19.8 и 19.9 являются математически завершенными, они, однако, требуют некоторых комментариев и интерпретации, изложением которых мы сейчас и займемся.

Во-первых, изображение оптимальной стратегии, представленное на рис. 24, показывает, что для достаточно высокого расклада оказывается pf = 1, т. е. игрок должен назначать обязательно высокую ставку.

Этот случай соответствует раскладам z > - Для младших раскладов,

однако, pf = Рз - 1 ~~ Pf = цп так что как Pi так и Рз отличны от нуля, т. е. игроку следует назначать беспорядочно высокие и низкие ставки (с определенными вероятностями). Этот случай соответствует

раскладам z rgj ~~ъ Высокие ставки (в этом случае) будут более редкими

чем низкие; действительно, £ = у , а а > 6. Эта последняя формула

показывает также, что последний тип высоких ставок становится все более редким, если размер высокой ставки (по сравнению с низкой) возрастает.

Теперь эти высокие ставки при младших раскладах, которые делаются беспорядочно (с определенными вероятностями) и которые становятся все более редкими с ростом цены высокой ставки, получают очевидную интерпретацию: они являются блефом в обычном покере.

Благодаря большим упрощениям, которые мы приняли при нашем анализе покера, блеф вошел в самом зачаточном виде, но тем не менее признаки его несомненны. Игроку целесообразно всегда назначать высокую ставку при старшем раскладе (z > (а - Ъ)1а) и, как правило, назначать низкую ставку (с вероятностью а/(а + Ь)) при младшем раскладе (z <С (а - Ъ)1а)\ вместе с тем иногда надо беспорядочно блефовать

(с вероятностью

19.10.2. Во-вторых, условия в зоне блефа, 0 rg z rg а-- , также

проливают некоторый свет на другие факты - на такие последствия отхода от оптимальной стратегии, как перманентная оптимальность , защита , нападение , как это рассматривалось в пп. 17.10.1, 17.10.2.

Предположим, что игрок 2 отклоняется от своей оптимальной стратегии, т. е. использует вероятности о*, которые могут отличаться от чисел pj, полученных выше. Кроме того, предположим, что игрок 1 тем не менее продолжает использовать вероятности pf, т. е. применяет оптимальную стратегию. Тогда мы можем воспользоваться gформулами (19:9:а*), (19:9:Ь*), (19:9:с*) из п. 19.7 для определения чисел у), графически пред-

ставленных на рис. 25, и с помощью (19:7*) из п. 19.7 вычислить выигрыш в игре для игрока 1:

(19:22) К=2 ]mdz-

з о

Поэтому используемые игроком 2 вероятности о) будут оптимальны против используемых игроком 1 вероятностей pf, если будет выполнено условие, аналогичное условию (19:8) из п. 19.6:

(19:С) Для каждой пары z, jf, для которой у) не достигает минимума

(по У *)), имеем of = 0. Иными словами, условие (19:С) необходимо и достаточно для того, чтобы вероятности о) были настолько хороши против р), насколько вероятности р) хороши против самих себя, т. е. дают К = 0. В противном случае вероятности о] плохи, т. е. дают К > 0. Иными словами:

(19:D) Ошибка, т. е. стратегия о), отличающаяся от оптимальной стратегии pj, не приведет к потерям, когда противник придерживается оптимальной стратегии, в том и только том случае, когда величины о? удовлетворяют приведенному выше условию (19:С).

Теперь достаточно мельком взглянуть на рис. 25, чтобы понять, что условие (19:С) означает, что of = af = 0 для z > (а - Ь)/а, но только af = 0 для z (а - Ъ)1а 2). Иными словами, условие (19:С) предписывает назначать высокую ставку и не делать ничего иного для старших раскла-

/ а - Ь\

дов ( z >> -у- 1 ; оно запрещает низкую ставку с последующим пасованием для всех раскладов, но его оказывается недостаточно для задания отношения вероятностей высоких и низких ставок (с последующим пасованием) для младших раскладов, т. е. в зоне блефа при z ~~~) *

19.10.3. Таким образом, любое отклонение от оптимальной стратегии, допускающее нечто большее, чем некорректный блеф, приводит к немедленным потерям. Этого достаточно для партнера, придерживающегося оптимальной стратегии. Некорректный блеф не приводит к потерям против партнера, использующего оптимальную стратегию; но партнер может причинить потери путем надлежащего собственного отклонения от оптимальной стратегии. Итак, важность блефа состоит не в фактической партии, разыгрываемой против оптимально действующего игрока, но в той защите, которую он дает против отклонений партнера от оптимальной стратегии. Это согласуется с замечаниями, сделанными в конце п. 19.2, и, в частности, с предложенной там второй интерпретацией блефа 3). Действительно, элемент неопределенности, создаваемой блефом, является именно тем типом ограничений на стратегию противника, о котором мы там упоминали и который анализировался в конце п. 19.2.

*) Мы имеем в виду минимум по /, а не по z, /!

2) В действительности можно было допустить даже of Ф 0 для одной точки z = --- .

Но вероятность этого изолированного значения z равна нулю, и его можно не рассматривать. См. замечание на стр. 223.

3) Все сказанное справедливо для рассматриваемой здесь формы покера. Другие точки зрения см. в п. 19.16.