Указанное выше сравнение изолированных игроков и коалиций п - 1 игроков (самые большие коалиции, которые кому-либо могут противостоять!) достаточно только для данной конкретной цели, состоящей в установлении важности коалиций в такой обстановке.

Следовательно, подходящая коалиционная стратегия имеет теперь большое значение.

Назовем игру Г существенной, если ее характеристическая функция v (S) имеет редуцированную форму v (S) ф 0 *).

27.4. Различные критерии. Неаддитивные полезности

27.4.1. Пусть задана характеристическая функция у(£), а мы хотим из ее редуцированной формы v (S) получить явное выражение для у (см. выше).

Число -у является общим значением всех v ((&)), т. е. выражений

1 71

вида у ((к)) + а\, что на основании равенства (27:4) равно - 2V((/)) 2)*

пз=1

Следовательно,

(27:8) 7=-2

В результате мы имеем:

(27:В) Игра Г является несущественной тогда и только тогда, когда

2 у((/)) =0 (т. е. у = 0), и существенной тогда и только тогда,

когда 2 v((;)) < 0 (т. е. у < 0) 3).

Для игры трех лиц с нулевой суммой, в обозначениях п. 23.1, мы

имеем v((l)) = - a, v ((2)) = - Ь, v ((3)) = - с, так что у = ~ А.

Поэтому для* игры трех лиц с нулевой суммой наши понятия существенности и несущественности сводятся к соответствующим понятиям из п. 23.1.3. Учитывая интерпретации этих понятий в обоих случаях, этого и следовало ожидать.

27.4.2. Можно сформулировать некоторые дальнейшие критерии несущественности.

(27:С) Игра Г является несущественной тогда и только тогда, когда

значения ее характеристической функции \(S) могут быть представлены в виде

для некоторой системы чисел aj, ..., a-Доказательство. В самом деле, на основании (27:2) это как раз и означает, что функция v (S) стратегически эквивалентна v (S) =

г) См. снова сноску 1 на стр. 269.

2) Итак, -у совпадает с р из сноски 3 на стр. 267.

8) Мы уже видели, что тот или другой случай должен иметь место, поскольку 2 ▼((/)) = 0 и у 0.

== 0. Поскольку функция v (S) редуцированная, то она является редуцированной формой v(iS), а это и означает несущественность последней.

(27:D) Игра Г является несущественной тогда и только тогда, когда

для ее характеристической функции v (S) в условии (25:3:с) из п. 25.3.1 всегда имеет место знак =, т. е. когда

v(S[}T) = v(S) + v(T) при S[\T = 0.

Доказательство. Необходимость. Функция v(S) указанного в (27:С) вида, очевидно, обладает этим свойством.

Достаточность. Повторное применение этого равенства дает знак = в (25:5) из п. 25.4.1, т. е.

v(.S1U--.U5,p) = v(51)+...4-v(5p),

если ..., Sp попарно не пересекаются.

Рассмотрим произвольное множество S, например S = (kt, ..., кр)* Тогда для Si = (ki), Sp = (kp) мы получаем

v(5) = v((ft1))+...+v((up))-

Таким образом, мы имеем

где а\ - v((l)), . . ., а?п = v((w)), так что игра Г является несущественной на основании (27:С).

27.4.3. Оба критерия (27:С) и (27:D) выражают, что значение для любой коалиции получается из значений для ее участников х) путем суммирования. Следует помнить, какую роль в экономической литературе играет аддитивность значения или, скорее, ее нередкое отсутствие. Случаи, в которых значение, вообще говоря, не аддитивно, являются наиболее важными, но они представляют серьезные трудности при любом теоретическом подходе к ним; и нельзя сказать, что эти трудности удалось где-либа действительно преодолеть. В этой связи следует вспомнить обсуждения таких понятий, как дополнительность, полное значение, дележ и т. д. Теперь мы приступаем к соответствующему этапу нашей теории; здесь существенно то, что мы обнаруживаем аддитивность только в неинтересном (несущественном) случае, в то время как игры, действительно представляющие интерес (существенные), имеют неаддитивную характеристическую функцию 2).

Читатели, знакомые с математической теорией меры, придут к следующему заключению: аддитивные функции v(S), т. е. несущественные игры, оказываются в точности функциями меры на множестве /, которые придают множеству / полную меру нуль. Таким образом, произвольные характеристические функции w(S) являются новым обобщением понятия меры. Эти замечания глубоко связаны с предыдущими замечаниями относительно экономического значения. Однако подробное рассмотрение этого вопроса увело бы нас слишком далеко 3).

А) Читатель понимает, что мы используем слово значение (значение для коалиции S) для обозначения величины v(S).

2) В данный момент мы, разумеется, занимаемся только некоторым частным аспектом нашей теории: мы рассматриваем только значения для коалиций, т. е. согласованных поведений, а не значения для экономических благ или услуг. Читатель заметит, однако, что эта конкретизация заходит не так далеко, как это может показаться: товары и услуги в действительности означают экономические действия при их обмене, т. е. означают согласованные поведения.

3) Теория меры появляется вновь в другой связи. См. п. 41.3.3.

27.5. Неравенства в случае существенности

27.5.1. Вернемся к неравенствам из п. 27.2, в частности к (27:7), *{27:7*), (27:7**). Для у = 0 (в случае несущественности) все, очевидно, тривиально. Предположим поэтому, что у > 0 (случай существенности).

Утверждения (27:7), (27:7*), (27:7**) описывают область возможных значений для v (S) при любом числе р элементов из S. Эта область значений изображена на рис. 30 для каждого р=0, 1, 2, . . ., п - 2, л - 1, п.

Можно добавить следующие замечания.

27.5.2. Первое. Установим, что в существенной игре, т. е. при у > 0, обязательно должно быть п 3. В противном случае формулы (27:7), ,(27:7*), (27:7**) (или рис. 30, который выражает их содержание) приводят

к противоречию: для п = 1 или nljfy (п-2)у f/j 3j п = 2 (п - 1)-элементное множе-

ство S имеет 0 или 1 элемент; сле-

довательно, его функция v (S) должна, с одной стороны, равняться у, а с другой, 0 или -7, что невозможо х).

Второе. Для наименьшего возможного количества участников в существенной игре, т. е. для п = 3, формулы (27:7), (27:7*), (27:7**) (или рис. 30) определяют все: они указывают значение функции v (S) для 0, 1, п - 1, п = 3 все возможные количества (См. также замечание на стр. 269.)

в п. 23.1.3, на основа-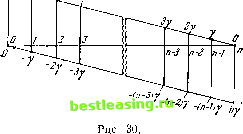

л-элементных множеств S; а для элементов следующие: 0, 1, 2, 3. Это согласуется с фактом, установленным

нии которого существует с нулевой суммой.

только один тип существенных игр трех лиц

Третье. Для большего количества участников, т. е. при п 7> 4, в задаче появляется новое усложнение. Как показывают формулы (27:7), (27:7*), (27:7**) (или рис. 30), количество элементов р множества S может теперь иметь значения, отличные от 0, 1, п - 1, п. Другими словами, интервал

(27:9)

рп - 2

становится теперь допустимым2). Именно в этом интервале указанные формулы не определяют больше единственного значения функции v (5); они устанавливают для него лишь интервал

(27:7)

PVv(S)(n - р) 7,

длина которого равна пу при любом р (см. снова рис. 30).

27.5.3. В связи с этим возникает вопрос: допустим ли в действительности весь интервал (27:7), т. е. не может ли он быть еще сужен при помощи дальнейших, более подробных исследований функции v(S)? Ответ

г) Конечно, в игре одного лица с нулевой суммой вообще ничего не происходит, а для игр двух лиц с нулевой суммой мы имеем теорию, в которой коалиции не возникают. Поэтому во всех этих случаях и следовало ожидать несущественность.

2) Можно взять п - 3 элемента, и это число положительно при п > 4.