нию к соответствующим понятиям в них, т. е. которое переводит эффективные множества, доминирование и решения для игры Г соответственно в эффективные множества, доминирование и решения для игры Г.

Эти рассуждения являются просто точной переработкой эвристических идей из п. 27.1.1, и читатель может подумать, что они не нужны. Однако в них приводится достаточно поучительный пример доказательства изоморфизма , и, кроме того, здесь снова могут быть применены наши прежние замечания о соотношении между описательным и точным доказательствами.

31.3.2. Пусть стратегическая эквивалентность задается числами a°v . . . , ап в смысле (27:1) и (27:2) из п. 27.1.1. Рассмотрим все дележи

а = {(*!, . . . , ап] игры Г и все дележи а = {а, . . . , ап} игры Т\ займемся поисками взаимно однозначного отображения

(31:15) а+±а

с нужными свойствами.

То, что соответствие (31:15) должно существовать, легко получить из рассуждений в начале п. 27.1.1. Мы описывали там переход от игры Г к игре Г при помощи включения в игру фиксированного платежа а& игроку к. Применение этого принципа к дележам означает

(31:16) ak-=ak + a0k для к=1, п1).

В соответствии с этим мы определяем отображение (31:15) при помощи равенств (31:16).

31.3.3. Проверим теперь требуемые свойства для отображения, определяемого посредством (31:15) и (31:16).

Дележи игры Г отображаются на дележи игры Г. В самом деле, эта означает, на основании (30:1) и (30:2) из п. 30.1.1, что свойства

(31:17) cti>v((0) Для i = l, /2,

(31:18) 2аг = 0

переходят в свойства

(31:17*) a-v((i)) для i = l, .... в,

(31:18*) 2 а. -0.

Это будет так для (31:17) и (31:17*), потому что v ((&)) = v ((&)) + a?

(вследствие (27:2) из п. 27.1.1.), для (31:18) и (31:18*), потому что 2 <*? =

г = 1

= 0 (на основании (27:1)).

Эффективность для игры Г переходит в эффективность для игры Г. В самом деле, на основании (30:3) из п. 30.1.1 это означает, что

2 ai = v (S) переходит в 2 ai = v ($) Это очевидно из сравнения (31:16) с (27:2).

х) Если мы введем (фиксированный) вектор a0 = {aj, . . . , an}, то равенства (31:16) могут быть записаны в векторной форме a = а + а0. Другими словами, это*

будет сдвиг (на а0) в векторном пространстве дележей.

Доминирование для игры Г переходит в доминирование для игры Г. Это означает то же самое для (30:4:а) - (30:4:с) из п. 30.1.1. (30:4:а) тривиально; (30:4:Ь) является эффективностью, котЬрая уже установлена; (30:4:с) утверждает, что at > р переходит в aj> Рь что очевидно. Решения игры Г отображаются на решения игры Г. В самом деле, это означает то же утверждение для (30:5:а), (30:5:Ь) (или (30:5:с)) из п. 30.1.1. Эти условия содержат только доминирование, которое уже установлено.

Сформулируем еще раз эти результаты:

<{31:Q) Если две игры с нулевой суммой Г и Г стратегически эквивалентны, то существует изоморфизм между их дележами, т. е. взаимно однозначное отображение дележей игры Г на дележи игры Г, которое оставляет инвариантными понятия, определенные в п. 30.1.1.

§ 32. НАХОЖДЕНИЕ ВСЕХ РЕШЕНИЙ СУЩЕСТВЕННОЙ ИГРЫ ТРЕХ ЛИЦ С НУЛЕВОЙ СУММОЙ

32.1. Математическая формулировка задачи. Графический метод

32.1.1. Обратимся теперь ко второй задаче, сформулированной m п. 30.4.1 и состоящей в нахождении всех решений для существенных игр трех лиц с нулевой суммой. Мы знаем, что такую игру можно считать заданной в редуцированной форме и что можно выбрать у = 1 1). Как мы установили прежде 2), характеристическая функция в этом случае полностью определена:

0 -1

(32:1) у(£) = когда S имеет

элементов.

Дележ является вектором

ar={ai, a2, a3},

три компоненты которого должны удовлетворять условиям (30:1) и (30:2) из п. 30.1,1, т. е. соответственно

(32:2) a1=t -1, a2=t -1, a3 -1,

(32:3) с + аз + осзО.

Мы знаем из (31:1) в п. 31.2.1, что эти компоненты а4, а2, а3 образуют лишь двумерный континуум, т. е. что они могут быть изображены на плоскости. В самом деле, условие (32:3) дает возможность сделать очень простое представление на плоскости.

32.1.2. Для этой цели возьмем на плоскости три оси, составляющие друг с другом углы в 60°. Для любой точки плоскости определим al7 a2, аз как ее расстояния по перпендикулярам до этих трех осей. Все расположение и, в частности, знаки, приписываемые компонентам ai9 a2, a3, приведены на рис. 31. Легко проверить, что для любой точки алгебраическая

2) См. рассуждение в начале п. 29.1 или приведенные там ссылки: конец п. 27.1 и второе замечание в п. 27.3.

2), См. рассуждение в начале п. 29.1 или второй случай в п. 27.5.

сумма этих трех расстояний равна нулю и что, обратно, любая тройка

= { 1, а2, а3}, для которой эта сумма равна нулю, соответствует некоторой, точке.

Итак, представление на плоскости на рис. 31 выражает в точности

условие (32:2); поэтому оставшееся условие (32:2) равносильно ограниче-

->

нию, наложенному на точку а в плоскости на рис. 31. Это ограничение, очевидно, состоит в том, что точка должна лежать на треугольнике или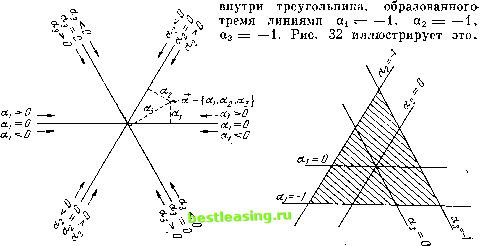

Рис. 31. Рис. 32.

Таким образом, заштрихованная область, которую мы называем

фундаментальным треугольником, представляет векторы а, которые удовлетворяют условиям (32:2) и (32:3), т. е. все дележи.

Рис. 33. Рис. 34.

W$ 32.1.3. Опишем теперь в этом графическом представлении отношение-доминирования. Так как п = 3, мы знаем из (31 :Н) (см. также обсуждение (31:8) в конце п. 31.1.5), что среди подмножеств S множества / = = (1, 2, 3) подмножества из двух элементов являются заведомо необходимыми, а все остальные - заведомо не необходимыми. Другими словами, множества, которые мы должны рассмотреть при нахождении всех, решений V, таковы: (1,2); (1,3); (2, 3). Таким образом, для

а = {аи а2, а3}, j3 = (р1э р2, р3}