Таким образом, при выбранном нормировании значение v (S) остается неопределенным только для двухэлементных множеств S. Обратим поэтому наше внимание на эти множества.

Множество / = (1, 2, 3, 4) всех игроков имеет шесть двухэлементных подмножеств:

(1,2), (1,3), (1,4), (2, 3), (2,4), (3,4).

Значения v (S) на этих множествах нельзя рассматривать как независимые переменные, так как для каждого из таких множеств S в этой же последовательности имеется дополнение. Именно, первое и последнее, второе и пятое, третье и четвертое соответственно дополняют друг друга. Поэтому их значения v (S) отличаются только знаком. Следует также вспомнить, что на основании неравенства (27:7) в п. 27.2 (с п = 4, р = 2) - 2 :=g v (S) 5g 2. Следовательно, если мы положим

у((1,4)) = 2*ь

(34:2) { v ((2, 4)) = 2ж2,

v ((3, 4)) = 2х3,

то будем иметь (34:3)

v((2,3))=-2*lf v((l, 3))=-2хг, y((i,2))=-2xa и, кроме того,

(34:4) - 1х19 х2, я3=2.1.

Обратно: если даны любые три числа xt, х2, х3, удовлетворяющие (34:4), то мы можем определить функцию v (S) (для всех подмножеств S из / = (1, 2, 3, 4)) по (34:1) - (34:3); однако мы должны еще показать, что эта функция v (S) является характеристической функцией игры. Согласно п. 26.1 это означает, что наше представление v (S) удовлетворяет условиям (25:3:а) - (25:3:с) из п. 25.3.1. В данном случае условия (25:3:а) и (25:3:Ь), очевидно, выполнены, так что остается проверить только условие (25:3:с). Из п. 25.4.2 следует, что нужно показать, что

v (St) + v (S2) + v (S3) =g 0,

если .Si, S2, S3 является разложением /. (См. также (25:6) в п. 25.4.1.) Если какое-нибудь из множеств Si, S2, S3 пусто, то два других являются взаимными дополнениями, и потому в условиях (25:3:а), (25:3:Ь) из п. 25.3.1 мы имеем равенство. Поэтому мы можем предполагать, что ни одно из множеств Si, S2, S3 не пусто. Так как всего в нашем распоряжении имеется четыре элемента, одно из множеств, скажем St = S, должно иметь два элемента, а два остальных являются одноэлементными. Таким образом, наше неравенство принимает вид

у(£) - 20, т. е. v(S)2.

Если мы запишем это неравенство для всех двухэлементных множеств S, то (34:2), (34:3) преобразуют его в следующие:

2*42, 2х2 2, 2х32,

- 2xi2, -2х22, -2х32,

что эквивалентно предположению (34:4). Таким образом, нами доказано следующее.

(34:А) Существенные игры четырех лиц с нулевой суммой (в их

редуцированной форме при выборе у = 1) в точности соответствуют тройкам чисел х2, х3, удовлетворяющих неравенствам (34:4). Это соответствие между игрой, т. е. ее характеристической функцией, и числами xz, х3 описывается уравнениями (34:1) - (34:3)

34.2.2. Проведенное выше представление существенной игры четырех лиц с нулевой суммой тройками чисел хи х2, х3 можно проиллюстрировать простым геометрическим рисунком. Мы можем рассматривать Х\, х2, х3 как декартовы координаты некоторой точки 2). В этом случае

неравенства (34:4) описывают часть пространства, точно заполняющую куб Q. Этот куб имеет центр в начале координат, а длина ребер равна 2, потому что шестью его гранями являются шесть плоскостей

-х, - I . j +л> Zi = ±l, х2=. ±1, #3=±1,

как это показано на рис. 41.

Таким образом, каждая существенная игра Г четырех лиц с нулевой суммой описывается ровно одной точкой внутри этого куба или Рис. 41. на его поверхности, и наоборот.

Представляется полезным именно так рассматривать эти игры и пытаться связывать их особенности с геометрическими условиями в Q. Особенно поучительным будет выделение игр, соответствующих тем или иным особенным точкам из Q.

Но перед тем, как приступить к осуществлению этой программы, мы рассмотрим некоторые вопросы симметрии. Мы хотим обнаружить связи между подстановками игроков 1, 2, 3, 4 и геометрическими преобразованиями (движениями) куба Q. В самом деле, согласно п. 28.1 подстановки соответствуют симметриям игры Г, а преобразования куба, очевидно, выражают симметрии геометрического объекта.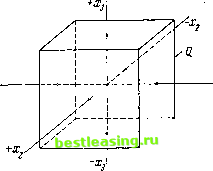

34.3. Перестановки игроков

34.3.1. При рассмотрении геометрического представления существенной игры четырех лиц с нулевой суммой нам пришлось ввести несколько произвольную операцию, т. е. операцию, которая частично нарушает симметрию исходной ситуации. В самом деле, описывая значения v (S) на двухэлементных множествах S, мы должны были выбрать три этих множества (которых всего шесть), чтобы получить координаты хи х2, х3. Мы так и сделали в (34:2) и (34:3), приписывая игроку 4 особую роль и устанавливая затем соответствие между игроками 1, 2, 3 и величинами xit х2, х3 (см. (34:2)). Таким образом, перестановка игроков 1, 2, 3 будет индуцировать такую же перестановку координат хи х2, х3, и в этих пределах система симметрична. Но таких перестановок только 6 из общего

г) Читатель может теперь сравнить наш результат с результатом п. 29.1.2, касающимся игр трех лиц с нулевой суммой. Можно заметить, как выросло разнообразие возможностей.

2) Мы можем также рассматривать эти числа как компоненты вектора в L3 в смысле п. 16.1.2 и след. Такой подход иногда будет удобнее, как в замечании на стр. 319.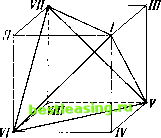

Рис. 42.

числа 24 всех перестановок игроков 1, 2, 3, 4 х). Поэтому подстановку, которая заменяет игрока 4 на другого, представить таким способом нельзя.

34.3.2. Рассмотрим одну из таких подстановок. По причинам, которые выяснятся немедленно, рассмотрим подстановку А, меняющую местами игроков 1 и 4, а также 2 и 3 2). Из уравнений (34:2) и (34:3) сразу следует, что эта подстановка не изменяет хи а х2 и х3 заменяются на -х2, -х3. Аналогично проверяется, что подстановка В, меняющая местами 2 и 4, а также 1 и 3, не изменяет х2 и заменяет х3 на - xi9 -х3. Наконец, подстановка С, меняющая местами 3 и 4, а также 1 и 2, не изменяет х3 и заменяет xi9 х2 на -xt,

Таким образом, каждая из трех подстановок А, В, С воздействует только на знаки переменных хи x2l х3, причем каждая изменяет ровно два знака, сохраняя третий. Так как эти подстановки заменяют 4 соответственно на 1, 2, 3, они при комбинировании их с шестью перестановками игроков 1, 2, 3 охватывают все перестановки игроков 1, 2, 3, 4. Теперь мы видим, что перестановки игроков 1, 2, 3 соответствуют шести перестановкам xi9 х2, х3 (без изменения знака). Следовательно 24 перестановки 1, 2, 3, 4 соответствуют шести перестановкам Xt, х21 х3, причем каждая из них либо не меняет знаков, либо меняет ровно два 3).

34.3.3. Мы можем также сформулировать это следующим образом. Если мы рассматриваем все движения в пространстве, переводящие куб в себя, то легко проверить, что они состоят из подстановок координатных осей Xi, х2, х3 в комбинации с некоторыми отражениями координатных плоскостей (т. е. плоскостей х2, х3; xi9 х3; xi9 х2). Математически - это перестановки xi9 х2, х3 в комбинации с некоторыми изменениями знаков

х2, #з- Всего существует 48 таких возможностей 4). Только половина из них, те 24, для которых число перемен знаков четно (т. е. О или 2), соответствует перестановкам игроков.

Легко проверить, что эти 24 возможности соответствуют не только преобразованиям куба Q в себя, но также, как показано на рис. 42, и тетраэдра /, V, VI, VII. Такое движение можно также охарактеризовать, замечая, что оно всегда переводит вершину куба Q, обозначенную черной точкой, в вершину, обозначенную черной точкой, и вершину, обозначенную светлой точкой, в вершину, обозначенную светлой точкой, но не переводит черную точку в светлую 5).

г) См. определения (28:А:а), (28:А:Ь) в пп. 28.1.1. 2) В обозначениях п. 29.1

/1, 2, 3, 4\ /1, 2, 3, 4\ /1, 2, 3, 4\

л-и,з,2.1Г * ~U4,i,2r °-U, 1,4,3;

3) Возможностей для таких изменений знаков в каждом случае имеется 1 + 3 = = 4, так что мы имеем 6 X 4 = 24 операции на xiy х2, х3 для представления каждой из 24 перестановок 1, 2, 3, 4 - как это и должно быть.

4) Для каждой из переменных, х2, х3 имеются две возможности: изменить знак или нет. Это дает 23 = 8 возможностей. Комбинация с шестью перестановками xi9 х2, х3 приводит к 8 X 6 = 48 операциям.

5) Данная группа движений хорошо известна в теории групп и особенно в кристаллографии, но мы далее не будем развивать этот подход.