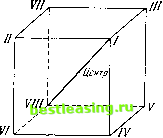Диагональ I-Цвнтр - VIII V/M / Центр

Рис. 43.

(заметим, что это дает (35:1) из п. 35.1.1 для xt = 1 и (35:6) из п. 35.2.1 для Xi = -1). Мы предполагаем, что xt больше, чем -1, но не очень намного; как велико может быть это отклонение, выяснится позже. Рассмотрим сначала эту ситуацию эвристически.

Так как предполагается, что xt не очень отличается от -1, рассуждения п. 35.2 могут все еще оставаться в силе. Образование двухэлементной коалиции из игроков 1, 2, 3 может даже теперь являться важнейшей стратегической целью, но не единственной: формула (35:7) из п. 35.2.1 перестает быть верной; вместо нее мы имеем

(36:2) v(S[}T)>v(S) + v(T),

если S П Т - 0

при Т = (4) 1). В самом деле, из (36:1) легко найти, что это превышение всегда равно 2) 2 (1 + Xi). Для xt = -1 оно обращается в нуль, но мы имеем xt немного > -1; поэтому это выражение немного >0. Заметим, что для упомянутой выше коалиции из двух игроков, куда не входит игрок 4, превышение в (36:2) 3), согласно (36:1), всегда равно 2 (1 - xt). Для х = -1 это выражение равно 4, а так как немного больше -1, то оно будет только немного меньше 4.

Таким образом, первая коалиция (из двух игроков, отличных от игрока 4) является намного более сильной, чем любая другая (где появляется игрок 4). Тем не менее последними коалициями не следует пренебрегать. Так как первая коалиция сильнее, можно ожидать; что она образуется с самого начала и что, как только она образовалась, она будет действовать как один игрок по отношению к двум оставшимся. Следовательно, можно ожидать, что в конце концов образуется некоторого рода игра трех лиц.

36.1.3. Если взять в качестве первой коалиции (1, 2), то предположительная игра трех лиц будет происходить между игроками (1, 2), 3, 4 4). В этой игре значения а, Ь, с из п. 23.1 равны

a = v((3,4)) = 2xlf b = v((l,2,4)) = l, c = v((l, 2, 3)) = 1 *).

Следовательно, если мы можем применить полученные там результаты (все это чрезвычайно эвристично!), то игрок (1, 2) получает величину a = (- а + Ъ + с)/2 - 1 - xt в случае успеха (в образовании* одной из последних коалиций) и -a = --2xi при неудаче. Игрок 3 получает

л) Если S = 0 или -Г. то в этом случае в (36:2) всегда имеет место знак =. То есть в рассматриваемой ситуации коалиция S должна состоять из одного или двух элементов.

2) Согласно предыдущей сноске S имеет один или два элемента и не содержит игрока 4.

3) То есть теперь S, Т - два одноэлементных множества, не содержащих игрока 4.

4) Можно было бы сказать, что игрок (1,2) - это юридическое лицо, в то время как игроки 3, 4 в нашем примере - физические лица.

5) Напомним, что во всех последующих формулах xt близко к -1, т. е. по предположению отрицательно; следовательно, - х± - это выигрыш, а х± - проигрыш.

величину р = (а - Ъ + с)/2 = xt в случае успеха и -Ъ = -1 при неудаче. Игрок 4 получает величину у = (а + Ъ - с)/2 = х± в случае успеха, и -с = -1 при неудаче.

Так как первыми могут являться коалиции (1, 3), (2, 3), так же как и (1, 2), вследствие тех же самых эвристических причин, что и при обсуждении игры трех лиц (в §§ 21, 22), можно ожидать, что партнеры в этих коалициях разделят выигрыш поровну. Таким образом, когда коалиция добивается успеха (см. выше), ее члены могут надеяться на выигрыш (1 - #i)/2 каждый, а в случае проигрыша - на xt каждый.

36.1.4. Резюмируем. Если наши предположения подтвердятся, то ситуация будет следующей.

Если первой является коалиция (1, 2) и ей удается найти союзника и если тем игроком, который соединяется в окончательной Коалиции с игроками 1, 2, оказывается игрок 3, то игроки 1, 2, 3, 4 получают соответственно выигрыши (1 - #i)/2, (1 - #i)/2, х±, -1. Если таким присоединяющимся к игрокам 1, 2 оказывается игрок 4, то эти величины заменяются на (1 - #i)/2, (1 - х±)/2у -1, х±. Если первая коалиция (1, 2) неудачна, т. е. если игроки 3, 4 объединяются против нее, то все игроки получают соответственно выигрыши -х±, -х хи х±.

Если первой является коалиция (1, 3) или (2, 3), то к приведенному описанию нужно применить соответствующую подстановку игроков 1, 2, 3.

36.2. Участок, примыкающий к вершине VIII. Точное описание

36.2.1. Теперь необходимо строго проверить все сказанное. Эвристический набросок, очевидно, соответствует следующему предположению. Пусть V - следующее множество дележей:

(36*3) а - -Г1- *1 1 ~Xi -1 # ЭТИХ пеРестановкои игроков

дележи, получающиеся из IX перестановкой игрок (т. е. компонент) 1, 2, 3

Об - { - Х\ч -х±У

(см. сноску 5, стр. 321). Мы ожидаем, что это множество V является решением в строгом смысле п. 30.1, если х± близко к -1; мы должны установить, так ли это и для какого именно промежутка изменения х±.

Установление этого (если вообще возможно) приводит к следующему результату.

(36:А) Множество V, состоящее из векторов (36:3), является решением в том и только в том случае, если -1 х± -1/5.

Это является ответом на вопрос, в каком по размеру промежутке (от начальной точки х± = -1, т. е. от вершины VIII) приведенное выше эвристическое рассмотрение приводит к правильному результату.

Замечание. Мы хотим подчеркнуть, что (36:А) не утверждает, что V является (в данном промежутке изменения х±) единственным решением рассматриваемой игры. Однако многочисленные попытки с аналогично построенными множествами найти другие решения для х -1/5 (т. е. в области (Зб:А)) потерпели неудачу. Для Xi немного >> -1/5 (т. е. немного выходящего за пределы (36:А)), где множество V из (Зб:А) больше не является решением, справедлив тот же результат для решения, которое его заменяет. (См. (36:В) в п. 36.3.1.)

Мы, конечно, не сомневаемся, что другие решения дискриминирующего типа, как обсуждалось неоднократно, всегда существуют. Но они совершенно отличны от конечных решений V, которые здесь рассматриваются.

По-видимому, именно эти аргументы оправдывают нашу точку зрения, что в природе решений имеется некоторое качественное изменение при

х±= -- (на диагонали 7-центр-У 7).

36.2.2. Доказательство (36:А) можно провести строго без какой-либо особой технической трудности. Оно состоит в несколько механическом перечислении ряда частных случаев и не проясняет принципиальной стороны вопроса Следовательно, читатель при желании может пропустить чтение доказательства, не теряя связи с основным направлением изложения. Он должен только помнить формулировку результатов в (36: А).

Тем не менее мы приведем доказательство полностью по следующей причине. Множество V из (36:3) было найдено эвристически, т. е. вообще без использования точной теории п. 30.1. Последующее строгое доказательство основывается только на теории п. 30.1 и посредством нее возвращает нас в конечном счете к единственно удовлетворительной точке зрения - к точной теории. Эвристические рассмотрения были только схемой для угадывания решения из-за недостатка лучших методов, и это - счастливая черта Точной теории, раз оказывается возможным угадать этим способом даваемые ею решения. Но такую догадку нужно затем проверить точным методом или, вернее, точный метод должен быть использован для определения того, в какой области значений дараметров догадка справедлива. Мы приводим строгое доказательство, чтобы дать возможность читателю подробно сопоставить и сравнить эти две процедуры: эвристическую и строгую.

36.2.3. Доказательство состоит в следующем.

Если Xi = -1, то мы находимся в вершине VIII и множество V из (36:3) совпадает с множеством, которое мы ввели эвристически (как решение) в п. 35.2.3, что легко можно строго проверить (см. также сноску 1 на стр. 315). Следовательно, теперь мы можем исключить этот случай и предположить, что

(36:4) *i>-1.

Мы сначала должны установить, какие из множеств S / = (1, 2, 3, 4) заведомо необходимы или заведомо не необходимы (в смысле п. 31.1.2), так как мы проводим доказательство как раз такого типа, который рассматривался там.

Непосредственно можно сделать следующие замечания:

(36:5) Вследствие (31:Н) в п. 31.1.5 трехэлементные множества S

заведомо необходимы, двухэлементные сомнительны, а все остальные заведомо не необходимы 2).

(36:6) Всякий раз, когда двухэлементное множество заведомо необходимо, мы должны исключить все трехэлементные множества, подмножеством которых оно является вследствие (31 :С) из п. 31.1.3.

х) Читатель может сопоставить это доказательство с доказательством, проводимым в связи с теорией игр двух лиц с нулевой суммой, например, комбинацию п. 16.4 с п. 17.6. Такое доказательство более прозрачно; оно обычно охватывает больше случаев и дает некоторое качественное разъяснение предмета и его связи с другими разделами математики. В ходе дальнейшего изложения теории такое доказательство встретится, например, в § 46. Однако большая часть теории все еще остается в примитивном и технически неудовлетворительном состоянии, типичными примерами чего являются последующие рассмотрения.

2) Ввиду того, что п = 4.