других, новая информация мгновенно отражается на котировках. Когда выясняется падение прибыли у General Motors или Merck объявляет о выпуске нового чудодейственного лекарства, котировки не стоят на месте в ожидании, пока инвесторы переварят информацию. Ни один инвестор не станет ждать, пока начнут действовать другие. На рынке действуют сворой, и новая информация немедленно изменит котировки акций General Motors или Merck. При этом сама новая информация поступает в случайном порядке. В силу этого изменения котировок непредсказуемы.

Интересные данные в поддержку этой точки зрения были приведены в 1950-х годах профессором Чикагского университета Гарри Робертсом. Роберте с помощью компьютера брал случайные числа из наборов с тем же средним и тем же средним квадратичным отклонением, какие наблюдались у цен на фондовой бирже. Затем он начертил диаграмму последовательной смены этих случайных чисел. Результаты оказались идентичными с результатами аналитиков рынков ценных бумаг, пытающихся предугадать движение котировок. Реальная динамика цен и динамика случайных чисел, выданных компьютером, оказались практически неразличимыми. Возможно, что и на самом деле биржевые котировки не имеют памяти.

Нормальность распределения - это жесткая проверка гипотезы случайных колебаний рынка. Но нужна одна важная оговорка. Даже если гипотеза случайных колебаний адекватно описывает ситуацию на фондовом рынке, даже если изменения котировок описываются нормальным распределением, среднее значение изменений всегда отлично от нуля. Тенденция к повышению котировок не должна нас удивлять. Состояние владельцев акций со временем растет, как и сбережения, доходы и прибыли корпораций. Поскольку по большей части котировки не падают, а растут, среднее значение их изменений оказывается положительным.

На практике для проверки предположения о нормальном распределении исследуемой совокупности случайных факторов применяются различные критерии согласия, устанавливающие соответствие между эмпирическим (опытным) и теоретическим (нормальным) распределением, и которые для задаваемой надежности (вероятности) позволяют принять или отвергнуть принятую гипотезу о нормальном законе распределения.

Нормальное распределение (распределение Гаусса) представляет собой вид распределения случайных величин, с достаточной

точностью описывающий распределение плотности вероятности результатов производственно-хозяйственной, финансовой, инновационной деятельности или изменений условий внешней среды, поскольку показатели, характеризующие их, определяются большим числом независимых случайных величин, каждая из которых в отдельности относительно других играет незначительную роль и непредсказуема. Применение нормального распределения для оценки рисков также связано с тем, что в основе данных, как правило, используется ряд дискретных значений. Эти теоретические предпосылки, а также апробация моделей для анализа рисков на основе нормального распределения доказывают адекватность этого теоретического инструмента реальным процессам экономической деятельности.

Плотность вероятности нормального распределения имеет вид:

(х-х)2

/(*) = -2сг , (3.6.3)

где х = а - математическое ожидание,

а - среднее квадратическое отклонение случайной величины X.

Из курса теории вероятностей известно, что попадание случайной величины X в заданный интервал (а; Р) определяется как

P(a<x<P) = j f{t)dt = ф

(3.6.4)

(х-х)2

2 dx

где ф(х) =-jL= \е 2°2

есть интеграл вероятностей или функция Лапласа, ее значения в зависимости от параметра х приводятся в специальных таблицах, эта функция четная и она изменяется от 0 до 0,5.

Если предположить, что ожидаемое значение результата (прибыль, потери и т.д.) должны принадлежать интервалу (а; Р) длиной Л = Р - а, то вероятность того, что достигаемый результат будет находиться в указанном интервале, определяется из формулы (3.6.4) и пусть равна Р\. На графике рис. 3.7 заштрихованная площадь численно равна Р\. Тогда вероятность попадания рассматриваемого результата за пределы допустимых границ, исхо-

дя из того, что вся площадь под кривой нормального распределения равна единице, будет равна Рг = 1 - Р\.

л А 1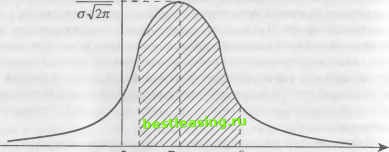

О а х-а р х

Рис. 3.7. Нормальная кривая

Вероятность Р2 оценивает неопределенность результата и отдельные авторы считают непосредственным измерителем риска величину Рг- На наш взгляд, лишь в относительно простых случаях для оценки степени риска можно использовать величину вероятности получения отрицательного результата (Рг), так как при этом не затрагиваются существенные факторы понятия риска, отсутствует сравнение возможных выигрышных исходов и обстоятельств, способствующих им, с возможными потерями в случае неудачи.

Средняя арифметическая х = а определяет центр распределения и ее размерность та же, что и размерность случайной величины X. Среднее квадратическое отклонение ст определяет разброс центра распределения и размерность ст совпадает с размерностью случайной величины X. На рис. 3.8 показано, как разница в значениях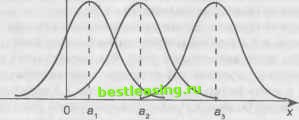

Рис. 3.8. Изменения в значении средней арифметической

средней арифметической влияет на положение графика, а на рис. 3.9 показано, как увеличение значения ст меняет размах кривой.

/fx) А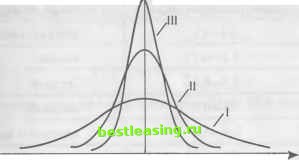

Рис. 3.9. Изменения в значении среднего квадратического отклонения

Параметр ст характеризует не положение, а самую форму кривой распределения. Это есть характеристика рассеивания. Наибольшая ордината кривой распределения обратно пропорциональна ст, при увеличении ст максимальная ордината уменьшается. Так как площадь кривой распределения всегда должна оставаться равной единице, то при увеличении ст кривая распределения становится более плоской, растягиваясь вдоль оси абсцисс; напротив, при уменьшении ст кривая распределения вытягивается вверх, одновременно сжимаясь с боков, и становится более иглообразной. На рис. 3.9 показаны три нормальные кривые (/, II, III) при а = 0; из них кривая I соответствует самому большому, а кривая / - самому малому значению ст. Изменение параметра стравносильно изменению масштаба кривой распределения - увеличению масштаба по одной оси и такому же уменьшению по другой.

В процессе принятия управленческих решений предпримате-лк> целесообразно различать и выделять определенные области (зоны риска) в зависимости от уровня возможных (ожидаемых) потерь. Для этого разработаны и используются так называемые шкалы риска, позволяющие классифицировать поведение лиц, идущих на хозяйственный риск. В табл. 3.11 приведена эмпирическая шкала риска, которую рекомендуют применять предпринимателям при использовании ими в качестве количественной оценки риска вероятность наступления рискового события авторы книги [50].

Таблица 3.11

Эмпирическая шкала допустимого уровня риска

Дадим математический анализ этой таблицы.

В практике общеупотребительной характеристикой рассеивания служит не среднее квадратическое отклонение а, а другая величина, называемая вероятным отклонением (иначе - срединным отклонением или срединной ошибкой ).

Вероятным отклонением называется половина длины участка, симметричного относительно центра рассеивания, вероятность попадания в который равна половине.

Геометрически вероятное отклонение Е есть половина длины участка оси абсцисс, симметричного относительно центра рассеивания, на который опирается половина площади кривой распределения (рис. 3.10).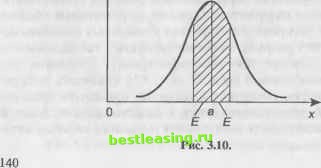

Вероятное отклонение мы будем обозначать буквой Е.

Поясним смысл термина срединное отклонение , часто применяемого в практике вместо вероятного отклонения . Вероя-ность того, что величина X отклонится от центра рассеяния а меньше чем на Е, по определению вероятного отклонения Е, рав-

Р(Х-а <£) = . (3.6.5)

Вероятность того, что это отклонение будет больше Е, также 1

равна -

Р{\Х-а\>Е)=±

Таким образом, при большом числе опытов в среднем половина значений случайной величины X будет отклоняться от а больше чем на Е, а половина - меньше; отсюда и термин срединное отклонение .

Из курса теории вероятностей известно, что вероятность того, что отклонение случайной величины X от среднего значения а по абсолютной величине не превысит положительного числа е = at, определяется соотношением

Р<\х-а\<е) = 2ф\ = 2ф(1)- (3.6.6)

Очевидно, вероятное отклонение как характеристика рассеивания должно находиться в прямой зависимости от среднего квад-ратического отклонения а. Установим эту зависимость. Для этого вычислим вероятность события \х-а\<Е в уравнении (3.6.5) по формуле (3.6.6)

Р(\Х-а\<Е) = Ф

( Е

о-л/2

\- (3.6.7)

Формулы (3.6.4), (3.6.6) и (3.6.7) применяются на практике для попадания случайной величины X в заданный интервал.

Для примера вычислим вероятности попадания случайной ве-