довательно, будет справедливой следующая формула, называемая формулой сложных процентов:

Р, = P{I + i)\

(4.11)

Pt - наращенная за время / (срок в периодах, соответствующий процентной ставке г);

коэффициент дисконтирования (процентная ставка в долях);

Р - основной капитал (текущая стоимость вклада).

Графики зависимости наращенного значения капитала от срока t для фиксированных процентных ставок приведены на рис. 4.2 (Р = 1).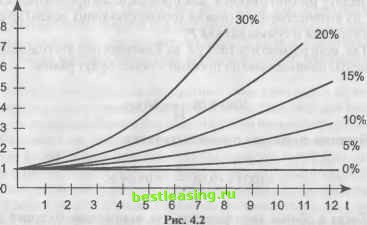

Для получения формулы наращения, когда проценты начисляются чаще, чем раз в год, необходимо изменить выражение (4.11). Годовая процентная ставка делится на количество периодов начисления в году, а степень t умножается на количество периодов начисления в году:

Р,=Р

1 + -

(4.12)

где т - количество периодов начисления в году.

До сих пор мы рассматривали случаи дискретного начисления процентов. Представляет интерес определить процент как результат непрерывного начисления.

В начальный момент времени имеется вклад Р. Поставим задачу добиться к концу года максимального роста этой суммы. Если банк дает г% годовых, то за год хранения вклад возрастет на г%, за любой меньший срок вклад возрастет пропорционально этому сроку, например, за один месяц прирост составит х1\г%, а за один день 7зб5%- Если представить себе (только теоретически), что операция открытия - закрытия вклада производится непрерывно, то можно рассмотреть следующую общую задачу.

Сумма Р, вложенная в банк под г% годовых, хранится t лет. Разделив отрезок [0; t] на п равных периодов, получим теоретически возможную конечную сумму:

Р. = limP 1 + ---j - ~ 100-и

= Plim

WOn ШО rl

rl 100

Таким образом, для конечной суммы вклада имеем формулу непрерывных процентов:

Р,=Ре =Р-еи, гДе = Ш-

(4.13)

Например, при годовой ставке г = 100% можно к концу второго года получить Р = Ре2 = Р 7,41, т.е. увеличить начальный вклад более чем в семь раз.

Пример 4.1. Найти разницу наращенных за два года значений на сумму 300 тыс. у.е. по ставке 10% при непрерывном и ежемесячном начислении процентов.

При непрерывном начислении процентов наращенная сумма будет:

Pt = 300-е0,22 =366,421 тыс. у.е., а при ежемесячном начислении процентов наращенная сумма равна:

Л2-2

р, =зоа i+

366,117 тыс. у.е.

и разница составляет:

366421 -366117 = 304 у.е.

Рассмотрим некоторые виды средних величин, которые широко применяются в финансовых операциях. Средние величины позволяют снижать имеющуюся информацию. Так, если в отрасли занято п человек и по каждому работнику имеется информация

о его доходах */,-, (i = l,n). то можно, например рассчитать среднюю зарплату по отрасли, вычислив величину:

d = J~, (4.14)

называемую средним арифметическим.

Можно также пользоваться и такой величиной, как среднее геометрическое. Пусть, например, имеются данные об индексах инфляции а, по каждому из п лет (/ = 1, и). Так как а, есть отношение уровня цен на конец /-го года к уровню цен на начало года, то за все п лет уровень увеличивается в (а7, а2 ... , а ) раз. Поэтому для определения среднего годового индекса цен лучше использовать среднее геометрическое, равное:

аг =ща2..лп . (4.15)

Отметим еще одну среднюю величину, которую называют средним гармоническим и равную:

С-1-р-Г (4-16)

- + - + ...+ -

1 2

Анализ показывает, что

а>аг, а>агар , а<аа, где аа - среднее квадратическое.

Пример 4.2. Пусть в течение 1-го, 2-го и 3-го годов цены увеличивались на 30%, а в течение 4-го и 5-го годов снижались на

45%. Среднее годовое изменение уровня цен за 5 лет, полученное с помощью среднего арифметического, составит

(30 + 30+30-45-45)=0%.

а среднее геометрическое изменение цен будет:

(5yj\,3-1,3 -1,3 -0,55 -0,55 -1) 100% = -7,85%.

Так как за пять лет уровень цен действительно понизился, то можно сделать вывод, что целесообразно применять среднее геометрическое при определении среднего индекса цен за ряд последовательных лет.

Рассмотрим другой пример. Пусть в обращении имеется п наличных рублей и tj, (i = 1, п) есть среднее время, в течение которого /-ый рубль находился в собственности одного человека. Среднее время, в течение которого каждый рубль принадлежит одному лицу, равно:

- = t1+t2+...+t п

Рассмотрим другой подход. Вычислим число оборотов каждого рубля за год по формуле *ч - - и найдем среднее арифмети-

ческое числа оборотов:

-Kl + K2+... + K п

и определим среднее время по формуле:

- 1 п

*~К~ 11 1 -+-+...+-

т.е. имеем среднее гармоническое оборота рубля.

Если за V принять суммарный объем всех операций за год с участием наличных денег, то связь между массой наличных денег п и объемом операций имеет вид:

n = t-V, где V = Kl + K2+...K .

Анализ показывает, что среднее время, рассчитанное как среднее арифметическое, является завышенной оценкой среднего времени, рассчитанного как среднее гармоническое.

4.2.4. Переменная процентная ставка

На практике может иметь место ситуация, когда процентная ставка будет изменяться в течение срока, на которой предоставляется ссуда.

Пример 4.3. С учетом реальной экономической ситуации в стране банк поставил следующие условия выдачи ссуды в сумме 10 млн у.е. на один год: за первые 60 дней ссудный процент равен 100%; за следующие 60 дней - 120%, за следующие 60 дней - 150%, за следующие 60 дней - 190%, за следующие 60 дней - 240% и за остальные 65 дней - 300%. Требуется определить сумму, возвращенную банку.

Если t\ - продолжительность 1-го периода ссуды, на котором используется ссудный процент г\, продолжительность 2-го периода t2, на котором используется ссудный процент г2 и т. д., то возвращаемую сумму можно определить так:

P,=fl

1 + f, -L- + t7 -=- + ..

1 100 2 100

= 10

60 100 60 120 + 365100 + 365100 +

60 150 60 190 60 240 65 300 ЛО + 3-ТШ + 3100 + 365 - ШО+ 365 100 J = 28493M y.e.

Пример 4.4. Цена на товар понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?

Так как проценты снижения равны г\ = 40% и г2 = 25%, то индекс снижения ц = 0,4 и i2 = 0,25. Новая стоимость товара составляет (1 - 0,4)(1 - 0,25) = 0,45 или 45% от старой, а поэтому цена товара понизилась на 100 - 45 = 55%.

Пример 4.5. За первый месяц цена товара возросла на 25%, а во втором месяце вернулась к прежнему уровню. На сколько процентов уменьшилась новая цена товара?

Если товар стоил 100 у.е., то после подорожания стал стоить 100(1+0,25) = 125 у.е., а затем, после снижения, стал опять стоить

100 у.е., т.е. его цена уменьшилась на l-y-100% = 20% .

Пример 4.6. За год цена товара в рублях возросла на 500%, а цена того же товара в долларах возросла на 20%. На сколько процентов изменился курс доллара по отношению к рублю?

Пусть товар стоил Р руб., а стал стоить (6Р) руб., т.е. его стоимость возросла на 500% или в 6 раз, в долларовом эквиваленте товар стоил D у.е., а стал стоить (1,2 D) у.е. Очевидно, что курс

доллара к рублю до инфляции составлял -, а после инфляции -

l,2D

5Р D

5Р D

100%

Следовательно, курс доллара к рублю стал составлять

: 500%, или повысился на 400%.

4.2.5. Риски процентных ставок .

Изменение уровня процентных ставок на финансовом рынке влечет колебания в цене обращающихся облигаций, причем повышение процентных ставок является причиной понижения цены и убытков держателя облигации. Риск при инвестировании, связанный с изменением процентных ставок, называется риском процентных ставок.

Стоимость любого финансового актива: акции, облигации, физического актива (недвижимости, оборудования) и др. определяется как текущее значение потока платежей, связанных с этим активом. Для облигаций поток платежей представляет собой обычную ренту, состоящую из выплат купонных процентов и возмещения номинальной стоимости. И тогда текущая стоимость облигации равна текущему значению такой ренты.

Пусть i - текущая рыночная процентная ставка, Р - номинальная стоимость облигации, к - купонная процентная ставка,