

 |
 |

|
Промышленный лизинг
Методички
процентных ставок, а стратегии работы с иностранными ценными бумагами - на ожидаемых обменных курсах валют. Пассивные портфельные стратегии требуют минимума информации о будущем. В основе таких стратегий лежит диверсификация портфеля, обеспечивающая максимальное соответствие его доходности выбранному рыночному индексу. Пассивные стратегии основываются на предположении, что вся доступная информация на рынке отражается в рыночных котировках ценных бумаг. При выборе активов необходимо указать соответствующие количественные характеристики, т.е. какие доли капитала инвестировать в различные типы и виды ценных бумаг. На этом этапе менеджер стремится сформировать эффективный портфель. Этот портфель представляет собой портфель, имеющий либо наибольшую ожидаемую доходность при заданном уровне риска, либо наименьший риск при заданной ожидаемой доходности. При оценке эффективности инвестиций производится вычисление реализованной доходности портфеля и сопоставление полученного результата с выбранным базисным показателем. Базисным показателем в данном случае служит некоторая количественная характеристика поведения заранее выбранного набора ценных бумаг. В качестве базисного показателя может быть выбран любой из общеизвестных фондовых индексов, например индекс Standard & Poors 500 (S&P 500), или один из облигационных индексов, публикуемых ведущими консалтинговыми компаниями. Важнейшую роль в управлении инвестициями играет теория оптимального портфеля, связанная с проблемой выбора эффективного портфеля, максимизирующего ожидаемую доходность при некотором, приемлемом для инвестора уровне риска. Теоретико-вероятностные методы позволяют дать определения ожидаемой доходности и риска портфеля, а статистические данные --получить оценку этих характеристик. При построении эффективного портфеля будем считать, что инвестор избегает риска, т.е. из двух вариантов инвестирования с одинаковой ожидаемой доходностью, но различными уровнями риска он выберет тот, риск которого меньше. Если инвестор стоит перед выбором одного из эффективных портфелей, то оптимальным портфелем будет наиболее предпочтительный из них. Гарри Маркович считается отцом современной портфельной теории , касающейся методов сбалансирования рисков и экономической выгоды при выборе направлений рискованных инвестиций. В своей программной статье [96] Выбор портфеля (Portfolio Selection), опубликованной в 1952 году в Journal of Finance, он разработал математическую модель, демонстрирующую, как инвесторы могут максимально снизить риск при заданной ставке доходности. Модель Марковича входит в основы финансов и широко применяется на практике специалистами по управлению инвестиционными портфелями. В 1952 г. Гарри Маркович опубликовал фундаментальную работу, которая является основой подхода к инвестициям с точки зрения современной теории формирования портфеля. Подход Марковича начинается с предположения, что инвестор в настоящий момент времени имеет конкретную сумму денег для инвестирования. Эти деньги будут инвестированы на определенный промежуток времени, который называется периодом владения. В кон-че периода владения инвестор продает ченные бумаги, которые были куплены в начале периода, после чего либо использует полученный доход на потребление, либо реинвестирует доход в различные ченные бумаги (либо делает то и другое одновременно). Таким образом, подход Марковича может быть рассмотрен как дискретный подход, при котором начало периода обозначается / = 0, а конец периода обозначается t = 1. В момент t = 0 инвестор должен принять решение о покупке конкретных ценных бумаг, которые будут находиться в его портфеле до момента t = 1. Поскольку портфель представляет собой набор различных ценных бумаг, это решение эквивалентно выбору оптимального портфеля из набора возможных портфелей. Поэтому подобную проблему часто называют проблемой выбора инвестиционного портфеля. Принимая решение в момент t = 0, инвестор должен иметь в виду, что доходность ценных бумаг (и, таким образом, доходность портфеля) в предстоящий период владения неизвестна. Однако инвестор может оценить ожидаемую (или среднюю) доходность различных ценных бумаг, основываясь на некоторых предположениях, а затем инвестировать средства в бумагу с наибольшей ожидаемой доходностью. Маркович отмечает, что это будет в общем неразумным решением, так как типичный инвестор хотя и желает чтобы доходность была высокой , но одновременно хочет, что- бы доходность была бы настолько определенной, насколько это возможно . Это означает, что инвестор, стремясь одновременно максимизировать ожидаемую доходность и минимизировать неопределенность, т.е. риск, имеет две противоречащие друг другу цели, которые должны быть сбалансированы при принятии решения о покупке в момент t = 0. Подход Марковича к принятию решения дает возможность адекватно учесть обе эти цели. Следствием наличия двух противоречивых целей является необходимость проведения диверсификации с помощью покупки не одной, а нескольких ценных бумаг. В 1990 году Нобелевская премия по экономике была присуждена ученым Гарри Марковичу, Мертону Миллеру и Уильяму Шарпу за научный вклад, оказавший огромное влияние на развитие теории и практики финансов. Далее вашему вниманию предлагается краткое описание их работ. Уильям Шарп использовал результаты исследований Г. Марковича в качестве отправного пункта для дальнейших исследований, в ходе которых определил влияние модели Марковича на чены финансовых активов. Сделав допущение, что в любой момент времени чены на финансовые активы будут изменяться, чтобы обеспечить равновесие спроса и предложения каждого рискованного актива, он продемонстрировал, что ожидаемые показатели доходности рискованных активов должны иметь очень спечифическую структуру ( Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk , Journal of Finance, 1964) ( Оченка акчий. Теория рыночного равновесия в условиях риска ). Структура активов, выведенная в теоретических построениях Шарпа, в наши дни очень широко используется в качестве основы для регулирования степени риска во многих областях теории и практики финансов. Основной вклад Мертона Миллера выражается главным образом в развитии теории корпоративных финансов. Совместно с другим ученым, Франко Модильяни (также лауреатом Нобелевской премии в сфере экономики), Миллер занимался вопросами дивидендной политики и политики заимствования фирм. Этим проблемам ученые посвятили серию статей, началом которой была работа The Cost of Capital, Corporation Finance, and the Theory of Investment)) ( Стоимость капитала, корпоративные финансы и теория инвестирования ), опубликованная в American Economic Review в 1958 году. Главным их открытием стало то, что они пред- ложили теоретикам и практикам в области финансов обратить особое внимание на то, каким образом на общую стоимость любой фирмы влияет ее дивидендная и финансовая политика. Так называемая теория М&М (теория Модильяни - Миллера), изложенная в их совместных работах, является основой современной теории корпоративных финансов. В 1997 году Нобелевская премия по экономике была вновь присуждена специалистам в области финансов. На этот раз ее лауреатами стали Роберт К. Мертон и Майрон Шоулз. Комитет по назначению лауреатов выдвинул для присуждения премии еще одного ученого, Фишера Блэка, чья преждевременная смерть в возрасте 57 лет в 1995 году, помешала ему разделить эту честь. Эти три человека открыли математическую формулу для вычисления стоимости опчионов и других производных ченных бумаг, которая оказала огромное влияние на теорию и практику финансов. Она широко известна под названием формулы Блэка - Шо-улза (Black-Scholes option pricing formula). Портфельная теория представляет собой статистический анализ, выполняемый с челью выбора оптимальной стратегии управления риском. С какой бы точки зрения ни рассматривать - домохозяйства, компании или иного экономического субъекта, использование портфельной теории заключается в выработке и опенке компромисса между доходом и издержками, связанными с уменьшением риска, что необходимо для определения оптимального образа действия данного субъекта. Если речь идет о семье, то в качестве определяющего критерия принимаются предпочтения в области потребления и риска. И хотя предпочтения изменяются со временем, механизмы и причины этих изменений не рассматриваются в портфельной теории. Портфельная теория акчентирует внимание на том, как из нескольких финансовых вариантов выбрать такие, чтобы максимизировать данные предпочтения. В челом оптимальный вариант выбора предполагает опенку компромисса между получением более высокой ставки доходности и увеличением степени риска инвес-тичий. Однако отнюдь не каждое решение, направленное на сокращение риска, приводит к уменьшению ожидаемой доходности. Бывают обстоятельства, при которых обе стороны, подписывающие контракт о переносе риска, могут уменьшить уровень своего риска, заплатив за это ровно столько, сколько стоит юридическое оформление контракта. Например, покупатель и продавец дома могут договориться и установить фактическую цену дома в момент подписания контракта, хотя сама передача прав собственности состоится только через три месяца. Такое соглашение служит одним из примеров форвардного контракта. Соглашаясь заключить такой контракт, обе стороны избавляются от неопределенности, связанной с колебаниями цен на рынке жилья в ближайшие три месяца. Таким образом, когда противоположные стороны воспринимают риск одного и того же события с разных точек зрения, для обеих лучше всего совершить перенос риска с помощью контракта, причем ни одной из сторон не придется нести, значительные расходы. Решения, связанные с управлением риском, принятие которых не влечет за собой затрат, являются скорее исключением из правил, чем нормой. Обычно для сокращения степени риска требуется сбалансировать необходимые для этого расходы и получаемые выгоды. Такой компромисс, пожалуй, более всего очевиден в решениях, принимаемых домохозяйством по поводу распределения его средств среди таких активов, как акции, ценные бумаги с фиксированным доходом и жилье. Первые формальные модели портфельной теории были разработаны для выработки именно этого типа решений в управлении риском. В этих моделях для вычисления соотношения между риском инвестиций и их ожидаемой доходностью используется распределение вероятностей. Ожидаемая доходность портфеля ценных бумаг определяется как среднее значение распределения вероятностей, а риск - как стандартное отклонение возможных значений доходности от ожидаемого. 6.2. ДИВЕРСИФИЦИРОВАННЫЙ ПОРТФЕЛЬ В экономике часто встречаются ситуации, когда субъект (физическое лицо или фирма) должен выбрать одну из альтернатив. Существует экономическая теория, которая занимается изучением процесса выбора, используя так называемую функцию полезности. Функция полезности описывает правило, по которому каждому из возможных вариантов выбора приписывается некоторое числовое значение. Чем больше это значение, тем больше полез- ность данного варианта выбора. Говоря проще, в теории портфеля функция полезности выражает предпочтения субъекта при пределенных отношенях к риску и представлениях об ожидаемых доходностях. В графической форме функцию полезности отражают кривые безразличия. На рис. 6.1 они обозначены через щ, щ, Щ. На горизонтальной оси откладывается значение риска, а на вертикальной - ожидаемые доходности. Кривые представляют собой наборы портфелей с различными комбинациями риска и доходности. Точки одной такой кривой определяют значение риска и доходности для данного уровня полезности. Рассмотрим, например, два портфеля и и ы* на кривой щ. Портфель и имеет большую доходность, но и больший по сравнению с и* риск. При этом инвестору безразлично, какой из них выбирать. Наклон кривой безразличия означает, что с ростом риска инвестор требует его компенсации большей доходностью. 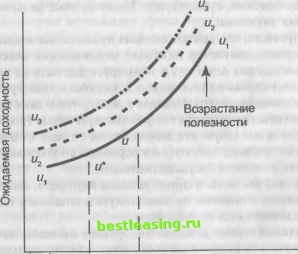 Риск Рис. 6.1. Кривые безразличия Чем выше лежит кривая, тем больше полезность, поскольку по вертикали отложены доходности. Таким образом, из трех кривых на рис. 6.1 кривая з имеет наибольшую полезность, а щ - наименьшую. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 [ 58 ] 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 |