ствует на обе бумаги в одну и ту же сторону. Диверсификация портфеля путем покупки обеих бумаг бесполезна - риск портфеля от этого не уменьшится.

При полной обратной корреляции возможно такое распределение вложений между различными видами ценных бумаг, что риск полностью отсутствует.

Полная обратная корреляция довольно редкое явление и обычно она очевидна.

Суммирая записанные выше отдельные элементы формализации, придем в общем случае к следующей оптимизационной задаче, которую решает инвестор: максимизировать доходность портфеля

Еп=х,Ец (6.7.7)

сведя риск (дисперсию) портфеля

п п

1=1 ;=1

к минимальному значению и выполняя естественное условие

5>,=1- (6-7.9)

Если инвестор только покупает ценные бумаги, то добавляется условие неотрицательности х, > 0.

Для инвестора, который готов участвовать в операциях типа коротких продаж, что равносильно взятию в долг суммы (-х,) под случайную ставку г неизвестные х, могут быть любого знака. Подобное заимствование сводится к тому, что инвестор продает акции, которых у него нет и которые он обещает поставить на оговоренную дату. При этом он назначает цену продажи, исходя из оценки будущего курса.

На дату поставки инвестор приобретает акции на реальном рынке и закрывает свои обязательства. Из-за возможного несоответствия цены приобретения ожиданиям инвестора вся операция сопряжена с риском процентной ставки г,- учитываемой в модели характеристиками е,-, оу\

Мы здесь не даем схемы коротких продаж, т.е. продаж ценных бумаг, которых в данный момент нет, рекомендуя обратиться к специальной литературе. Для нас важно только то, что если некоторые переменные ху окажутся отрицательными, то это будет означать, что по данным позициям следует участвовать в подобных операциях.

Очевидно, что точка (хь ... х ), доставляющая максимум полезности U (е, а), принадлежит множеству таких допустимых точек задачи (6.7.7) - (6.7.9), которые не могут быть улучшены сразу по двум критериям - е и ст. В теории многокритериальной оптимизации такие решения называются Парето-оптимальными, или эффективными.

Чтобы пояснить смысл этого понятия, представим себе контур, соединяющий точки с координатами с, ст, вычисленными для допустимых точек некоторого условного множествах (рис. 6.18).

Рис. 6.18. Восходящая дуга АВ соответствует Парето-оптимальному множеству решений

Множеству эффективных точек соответствует восходящая дуга АВ: для любой посторонней точки, например С, можно построить улучшающую ее точку (*) в том смысле, что либо е* > е, ст* = ст (точка С\), либо е* - е, а* < о (точка С2), либо е* > е, о* <а (точка Сз), а для своих точек этого сделать нельзя.

В связи с этим ясно, что поиск оптимального по критерию полезности U (е, а) портфеля можно проводить в два этапа: вначале, решая задачу (6.7.7) - (6.7.9), найти множество эффективных портфелей, а затем из этого множества отобрать портфель с максимальным уровнем полезности. Очевидно, что это может быть сделано с помощью множества эффективных точек.

Функция полезности U (е, а) и оптимальность по Парето будут подробно рассмотрены в следующей главе.

На данном этапе достаточно лишь знать, что у инвестора имеется некоторая функция полезности U (е, о), с помощью которой он может анализировать варианты, причем предпочтение отдается варианту с большим значением этой функции.

6.7.2. Построение границ эффективности портфеля

Известно, что если коэффициент корреляции в парах активов меньше чем 1,0, то диверсификация может улучшить взаимосвязь между ожидаемым риском портфеля и ожидаемым доходом по портфелю. Это происходит потому, что, если переменная доходности является линейной функцией средней доходности, то фактор риска представляет собой квадратическую функцию дисперсии доходов по ценным бумагам. Степень улучшения портфеля зависит от весов, которые каждый из активов имеет в портфеле, и от корреляции этих активов.

Лучший способ продемонстрировать это - пример с двумя активами. Рассмотрим данные табл. 6.8 - различные средние

Таблица 6.8

квадратические отклонения портфеля, составленного из двух рискованных активов, при допущениях, что корреляция pi?2 равна 0,6 или 0,9 и что доли каждого актива в портфеле меняются на 10%. Рис. 6.19 - это диаграмма границ эффективности, относящихся к портфелям, построенным с учетом предположенных pi2 = 0,60 и = 0,90. Актив 1 имеет ожидаемый доход 8% со средним квадратическим отклонением 12%, а актив 2 - ожидаемый доход 12% со средним квадратическим отклонением 16%.

Средние квадратические отклонения портфеля вычисляются по формуле (6.7.2).

Для предположенной степени корреляции среднее квадратическое отклонение рассчитано для некоторых различных портфелей, которые могут быть построены из этих двух активов и нанесены на диаграмму (рис. 6.19).

Сначала рассмотрим данные в столбце табл. 6.8 для ри = 0,6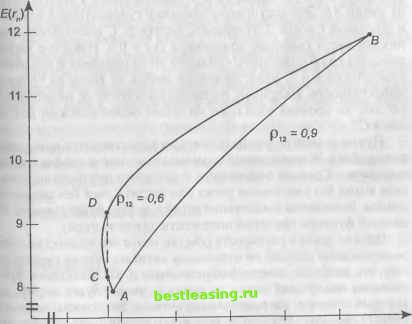

11 12 13 14 15 16 о-п

Рис. 6.19. Границы эффективности

и график на рис. 6.19 для рп - 0,6, отражающие выгоды от диверсификации для случая, когда активы умеренно коррелированны. Данные и график, обозначенные р\г = 0,9, показывают, что диверсификация имеет благотворное влияние на соотношение риск-доход, даже когда активы высоко, но не полностью коррелированны. Заметьте, что в обоих случаях граница эффективности вогнута. Чем больше степень вогнутости, тем больше выгоды от диверсификации. Учтите, однако, что не все точки на границе эффективны, а эффективна только верхняя часть каждой вогнутой границы (обозначенных АВ на рис. 6.19).

Верхняя часть каждой из линий А В представляет границу эффективности возможных портфелей, так как на границе невозможно достичь большего дохода без несения большего риска. Выше линии находится область недостижимых комбинаций риска и дохода из-за ограниченности характеристик ценных бумаг 1 и 2. Ниже линии находятся худшие комбинации риска и дохода, которые могут быть улучшены просто перемещением в любую точку на линии АВ. Это достигается продажей существующих активов и покупкой 1 и/или 2. Например, портфель С располагается на нижней части границы, помеченной рп - 0,6. Инвестор может повысить свою полезность продажей этого портфеля и покупкой комбинации 1 и 2, представленной любой из точек на границе эффективности. Например, перемещаясь в точку D, инвестор несет тот же уровень риска, но получает более высокий доход, чем в С.

Нужно отметить, что не существует единственного наилучшего портфеля. Жирные линии указывают на многие эффективные портфели . Граница эффективна, потому что невозможно повысить доход без увеличения риска или снизить риск без снижения дохода. Возможная комбинация риска и дохода будет зависеть от целевой функции (функция полезности для инвестора).

Однако давая в реальности обычно менее чем полностью коррелированные доходы по отдельным активам, теория предполагает, что наиболее диверсифицированным и, следовательно, приносящим наилучший доход на единицу риска, будет портфель, который содержит все рискованные активы. Это должны помнить инвестиционные менеджеры, поскольку их портфели обычно ограничены до содержания только денежных средств, облигаций и обычных акций.

6.7.3. Задача оптимизации портфеля

Теперь, понимая взаимосвязь между риском и доходом и влияние ковариации, мы можем определить задачу оптимизации портфеля. Задача оптимизации портфеля заключается в том, чтобы определить, какая доля портфеля должна быть отведена для каждой из инвестиций так, чтобы величина ожидаемого дохода и уровень риска оптимально соответствовали целям инвесторов. Предположим, что цель инвестора состоит в минимизации риска портфеля, где риск измеряется дисперсией портфеля.

На практике инвестор обычно устанавливает ограничения относительно способа, по которому может быть построен портфель. Например, целевой функцией может быть минимизация риска, но при каком-то минимальном уровне дохода, а также при ограничениях на минимальные и максимальные доли, которые могут быть инвестированы в каждый актив. Как поступать с этими ограничениями - объясним позже.

Сейчас же проиллюстрируем портфельную задачу, рассмотрев оптимизацию при ограничениях для случая портфеля из трех активов.

Требования инвестора обычно ограничивают процесс выбора. Например, инвестор может потребовать минимизации риска при ожидаемом доходе не менее или равном данному уровню.

Портфельная задача, таким образом состоит в минимизации дисперсии портфеля при каком-то минимальном уровне дохода. Из (6.7.4) видно, что дисперсия портфеля оп может быть выра-

жена через произведение транспонированного вектора V, т.е. V , дисперсионно-ковариационной матрицы Q и вектора V, т.е. V. Следовательно, поставленная задача является задачей квадрати-ческого программирования и может быть записана следующим образом.

Минимизировать функцию

Z = o-2=VrQV (6.7.10)

при ограничениях

fv,+v2+v3 =1

У,Е(г,) + V2E(r,) + V3E(r3) > Епр (г), (6 7 , {)

V, >0,V2>0,V3 >0,

где ЕПр{г) - это минимальный приемлемый уровень дохода.