

 |
 |

|
Промышленный лизинг
Методички
(6.8.15) (6.8.16) Оценкой портфеля называют ряд чисел (сгх), Е(х)), которую можно изобразить точкой на плоскости оЕо. Плоскость (о2, Е) называют критериальной. Меняя портфель, то есть меняя вектор х, получают различные оценки, а для них разные точки на критериальной плоскости. Множество всех оценок (то есть множество пар (о2, Е), а не множество портфелей) допустимых портфелей называют критериальным множеством. Если критериальное множество не сводится к одной точке, то возникает проблема выбора. Пусть П0 - некоторый портфель, а Qo - (a2, Eq) - оценка для По. Критериальную плоскость можно разделить на четыре квадранта (рис. 6.23). Если какой-то другой портфель П, имеет оценку в четвертом квандранте, то П] лучше По, так как Е\ > Е0 и oi2 < оо2. Если оценка для П, попадает во второй квандрант, то П, хуже По, так как Ех < £0 и а2 > ао2 (причем для обоих этих 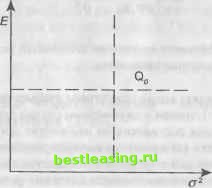 Рис. 6.23. Соотношение портфелей в критериальной плоскости квандрантов хотя бы одно неравенство в приведенных парах неравенств - строгое). Если же оценка Qi портфеля П, находится внутри (не на пунктирах рисунка) первого или третьего квандрантов, то имеем два таких портфеля, у которых один показатель лучше, чем у другого, но зато второй - хуже. Из выражения (6.8.15) найдем, что Еп-Е2 а затем после подстановки этого значения / в выражение (6.8.16) получим г о2Ех -алЕ ,с2 ах -с2 + ---ьп Ех -Е2 (6.8.17) Критериальное множество (6.8.17) является параболой на плоскости (от/, Еп) (рис. 6.24). 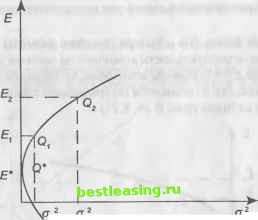 Рис. 6.24. Критериальное множество при р = 1 для двух активов Так как Ол2> О, то есть такой портфель, у которого риск нулевой. Приравнивая (6.8.17) к нулю, имеем Еп = Eit + Е2(\ -t) = E2 + (Ei - E2)t, риск портфеля 2 2 °n = X X ** *;cov(r О)= ,=1 у=1 = cxt2 +2pa1cT2t(l-t) + a2(l-t)2 = = (a,2-2pci02 +o2)t2 + 2(раха2 -c\)t+o\. Нулевой риск (точка (О, Е*) на графике) -г- это, конечно, хорошо, но одна из компонент х* - отрицательная величина, то есть заемные средства. Более того, может быть Е* < 0, так будет либо при 1 > о21о\ > М2/Ми либо при 1 < а21о\ < М21М\. Подобное устранение риска бессмысленно, поскольку означает гарантированный убыток (рис. 6.25). 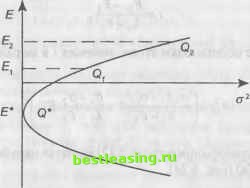 Рис 6.25. Гарантированный убыток при использовании заемных средств В модели Блэка (то есть при наличии заемных средств, что равносильно отрицательности компоненты векторах) может быть случай, когда Е* > 0, причем возможно, что доходность портфеля как понизится, так и повысится по сравнению с доходностями используемых активов (рис. 6.26, 6.27).
Рис. 6.26. Понижение доходности портфеля Так для случая, изображенного на рис. 6.27, имеем Ех < Е2, сг\ > 02, следовательно  > Рис. 6.27. Повышение доходности портфеля Возможно еще одно геометрическое представление для двумерного случая: при использовании стандартного отклонения ст = Л/о-2~ = о-2 +(а,-o2)t\ и ЕП=Е2 +(£]-E2)t получаем параметрическое задание критериального множества на плоскости (о2, Е) (рис. 6.28), которое будет парой лучей с верши-   Рис. 6.28. Критериальное множество ной в точке (о2, Е). Таким образом, для р = 1 критериальное множество - парабола на плоскости (о2, Е) или пара лучей на плоскости (о2, Е), минимальная граница совпадает с критериальным множеством, эффективная граница оценок - верхняя ветвь параболы на плоскости (о2, Е) или верхний луч на плоскости (о2, Е). Пусть для модели Блэка р = 0. В этом случае: Еп = Ег + (Еу - E2)t, од2 = о, V + Ог2(1 - г2) > 0. (6.8.19) Можно опять выразить t через Еп, подставить в On и получить зависимость ап от Еп, эта зависимость будет, как в предыдущем случае, квадратичной. /Для нахождения min on (теперь 2 do2-! оп > 0 строго!) решим уравнение -= 0 : = 2(ст2г -о\(1 - 01=f)->. t* = f2 , g (0; 1), at rrf O, + СЧ что дает: ого2 °l (*) = о \ +oi,0<o2n (r*) < min{o-2; o\} o i +o2 E,ol + E2ol о , +<7 Риск портфеля меньше риска каждого из активов, но устранить его полностью нельзя. Как и в предыдущем случае: минимальная граница совпадает с критериальным множеством, эффективная граница - верхняя ветвь параболы на плоскости (о2, Е) (рис. 6.29). При р = -1 получаем: ЕП=Е2+(Е1 -E2)t,an =оу-ст2(1-0 . (6.8.20) Рис. 6.29. Критериальное множество для некоррелированных активов Анализируя зависимости (6.8.20), получим кривые рис. 6.30 и рис. 6.31, но ,* = е(0;1) а, +о2 и £?* лежит внутри дуги 6162- Е2 Щ* Рис. 6.30. Случай р = -1 для модели Блэка на плоскости (сг2, Е) 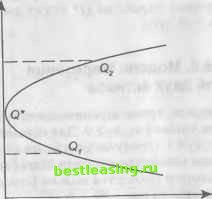
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 [ 78 ] 79 80 81 82 83 84 85 86 87 88 89 90 |