координаты вектора ж удовлетворяют соотношению

2>;£>,- = Д>. (10.2)

Условия (10.2) - это система р линейных алгебраических уравнений относительно q неизвестных. Считается, что р < q. Во-вторых, координаты векторов ж неотрицательны:

хх > 0, ж2 > 0, xq > 0. (10.3)

Множество векторов ж, удовлетворяющих условиям (10.2) и (10.3), называется многогранным множеством задачи линейного программирования. Обозначим это множество через Г.

На рис. 10.1 показано, как могут выглядеть множества Г для случая q = 3. Рисунок 10.1, а соответствует значению р = 1; множеством Г является треугольник ABC. Рисунки 10.1, б, в соответствуют значению р - 2; множествами Г являются отрезки АВ.

Множество Г может быть как ограниченным, так и неограниченным. (Все множества Г, показанные на рис. 10.1, являются ограниченными.) Если множество Г ограниченное, то задача линейного программирования всегда имеет решение. Если множество Г неограниченное, то задача линейного программирования может или иметь решение, или не иметь решения.

Нетрудно понять, что если задача линейного программирования имеет решение, то среди тех точек ж, удовлетворяющих условиям (10.2) и (10.3), для которых значение функции L(x) является максимальным, присутствует хотя бы одна вершина множества Г. Поэтому задача линейного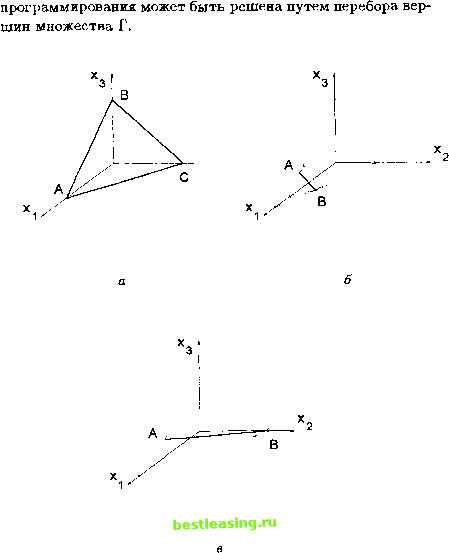

Рис. 10.1. Примеры многогранных множеств задач линейного программирования

Глядя на рис. 10.1, отвечающий случаю q = 3, можно подумать, что задача перебора является совсем простой. Однако это не так, и при больших q решение задачи линейного программирования требует применения достаточно сложных математических методов.

Описание этих методов дано, например, в [21], [27], [39]; там же можно найти доказательства приводимых ниже утверждений. Мы не будем рассматривать все сложные случаи и все варианты, а дадим описание только основной схемы симплексного метода для решения задач линейного программирования. Хотя это описание содержится во многих книгах, мы все же приведем его, поскольку без этого будет невозможно изложить симплексный метод для решения задач квадратичного программирования.

Будем предполагать, что выполняется следующее условие.

Условие невырожденности. Все вершины множества Г имеют р положительных координат и (q - р) нулевых координат.

Множества Г, изображенные на рис. 10.1, а, б, удовлетворяют условию невырожденности. Множество Г, изображенное на рис. 10.1, в, условию невырожденности не удовлетворяет, так как у точки В две нулевые координаты, а д-р = 3- 2 = 1.

Симплексный метод решения задачи линейного программирования состоит из двух этапов.

Этап 1. Нахождение одной из вершин многогранного множества Г.

Этап 2. Последовательное улучшение вершины множества Г, т. е. переход от найденной вершины к некоторой другой вершине, для которой значение функции L больше.