§ 3. Эффективный фронт и эффективные портфели

Напомним, что на рынке существует п видов ценных бумаг, доходность j-й ценной бумаги является случайной величиной Rj. В этом параграфе мы будем считать, что все ценные бумаги являются рисковыми, т. е. D(Rj) > О при j = 1,2,...,п. Наличие безрисковых ценных бумаг, т. е. ценных бумаг с точно предсказуемой доходностью, меняет ситуацию. Портфели, куда включаются безрисковые ценные бумаги, будут рассмотрены в §4.

Начнем со случая п = 2, т. е. когда портфель составляется из двух видов ценных бумаг. Для каждой из ценных бумаг известны ожидаемые доходности Ег и Е2 и стандартные отклонения доходностей ах и а2. Портфели с какими ожидаемыми доходностями йис какими стандартными отклонениями доходностей а могут быть получены путем комбинации этих двух ценных бумаг? Будем использовать следующие обозначения:

Х\ = /i, х2 = 1 - ц.

Тогда для портфеля, определяемого парой чисел х\,х2, доходность

R - piRi + (1 - fi)R2. Отсюда ожидаемая доходность

Е = цЕ1 + {1-ц)Е2,

Дисперсия

о3 = \i2D(Rx) + (1 - fi)2D(R2) + 2/i(l - rfCoviRt, R2) =

Теория эффективных портфелей ценных бумаг

где pi2 - корреляция случайных величин R\ и R2.

Напомним, что корреляция по абсолютной величине не может превосходить 1, т. е. -1 < р12 < 1.

Полученные уравнения для Е и а2 при изменении /л от -оо до +оо определяют некоторую кривую на плоскости (<т, Е). Будем считать, что Ei ф Е2, поскольку при Ег = Е2 все точки интересующей нас кривой находятся на прямой Е = Е\. Из уравнения для Е находим

Е - Е2 Ei - Е2

Подставляя это выражение в уравнение для сг2, видим, что изучаемая кривая является кривой второго порядка на плоскости (<т, JS), уравнение которой имеет вид

-(Et-Etf а2 +

+({<?!-<т2)2 + 2(1-р12) аха2) Е2 +

+2{{Е! + Е2) р12 ах <*2 - Е2а\ - Еха\) . Е +

+(Е2а2 + Е2а2-2Е1Е2р12а1(т2) = 0.

При классификации кривых второго порядка основную роль играет знак определителя матрицы, составленной из коэффициентов при членах второго порядка (см., например, [25], с. 64 - 65). В данном случае эта матрица имеет вид

-(Ei - Е2)2 0 \

0 (oi - <г2)2 + 2(1- р12) аха2 )

При о\ ф (т2 или /9i2 < 1 определитель этой матрицы отрицателен, т. е. данная кривая является гиперболой или парой пересекающихся прямых. Если а\ = а2 и р12 = 1, то, как

нетрудно увидеть, все точки интересующей нас кривой находятся на прямой а - а2.

Более детальный анализ показывает, что данная кривая является гиперболой при -1 < р12 < 1 и является парой прямых при = ±1. Подробно теория кривых второго порядка на плоскости описана, например, в [31].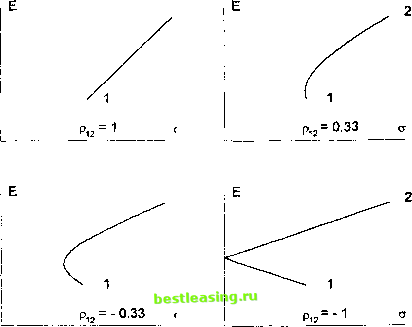

Рис. 3.1. Возможные сочетания рисков и ожидаемых доходностей для портфелей, составленных из двух ценных бумаг

На рис. 3.1 показаны возможные виды зависимости сг от Е для портфеля, составленного из двух ценных бумаг,