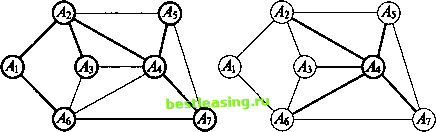Рис. 5ж Рис. б

Введем одно полезное понятие: множество всех ребер, выходящих из вершины графа, будем называть звездой этой вершины. На рис. 6 изображена звезда вершины А4.

Всюду в дальнейшем будем считать, что заданный граф связен, конечен и не имеет петель (начало ни одного ребра графа не совпадает с его концом).

Часто приходится рассматривать задачи, в которых каждому ребру заданного графа приписано некоторое положительное (неотрицательное) число (его вес). Обычно граф, нагруженный подобным образом, называют сетью, его вершины узлами, а ребра дугами.

В зависимости от приложений описанная числовая нагрузка дуги графа может иметь разный смысл и обозначать длину, стоимость, пропускную способность, временную протяженность и т.д.

Рассмотрим несколько характерных задач.

3.2. Минимальное порождающее дерево

Предположим заданным граф, числовые нагрузки (веса) дуг которого можно интерпретировать как их длины.

Выше уже отмечалось, что порождающих деревьев у графа может быть много. В рассматриваемом случае с каждым порождающим деревом естественно связать число, равное сумме длин всех его дуг. Ясно, что среди этих порождающих деревьев есть хотя бы одно, сумма длин всех дуг которого минимальна. Такое дерево называют минимальным порождающим деревом, minimum scanning tree, или минимальным остовом.

Начнем с рассмотрения двух примеров.

Пример 1. Имеется 7 городов А\, Аъ A3, Л4, As, As, А7, которые нужно связать между собой наиболее дешевой сетью дорог, если известно, что стоимость с (Ah Ак) сооружения участка дороги, соединяющей города А, и Ак (/, к = 1, 7, к), пропорциональна ее длине (рис. 7).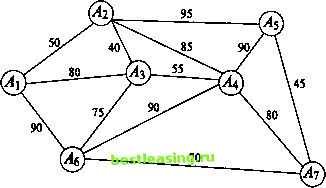

Рис. 7

Замечание. Граф наиболее дешевой соединяющей сети непременно должен быть деревом. (Если бы это было не так, то в графе нашелся хотя бы один замкнутый путь. При удалении любого из ребер этого замкнутого пути стоимость сети уменьшилась бы, а города все еще оставались соединенными.) Тем самым число ребер искомого графа в предложенном примере должно быть равным 6.

Поиск решения можно начать с любого узла. Пусть это будет узел А{.

1-й шаг. Самая короткая дуга, выходящая из этого узла, - это дуга (Аи А2) длины 50. Соединим узлы А{ и А2 жирной линией, как показано на рис. 7а, и пометим узлы Ai и А2.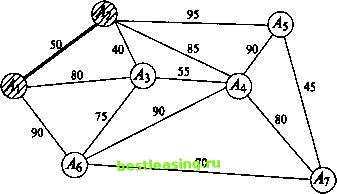

Рис. 7а

2-й шаг. Самой короткой дугой, выходящей из помеченных узлов А{ и А2 в еще непомеченные, является дуга (А2, Аг) длины 40. Добавим ее к дереву, выделив жирной линией (рис. 76).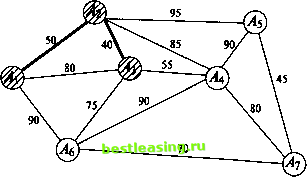

Рис. 76

3-й шаг. Узел Ал расположен к тройке Аи A2i А3 ближе всех других непомеченных узлов. Выделив дугу (А3, АО длины 55, переведем этот узел в помеченные (рис. 7в) и пометим узел А+.

Рис. 7в

4-й шаг. Следующим узлом будет узел As, расположенный к помеченной четверке Аи Аъ Л3, А+ ближе непомеченных узлов А5 и А7. Выделим дугу (у43, As) длины 75, соединяющую его с узлом А3 (рис. 7г), и пометим узел As.

5-й шаг. Узел А7, ближе узла А5 к пятерке помеченных узлов. Выделим дугу (As, А7) длины 70, соединяющую его с ближайшим узлом As (см. рис. 7д), и пометим узел А7.

6-й шаг. Оставшийся непомеченным узел А5 соединим с узлом А7 дугой (А5, А7) наименьшей длины 45 (рис. 7е) и также пометим его.

Поведем итог: шесть выделенных дуг связывают все семь узлов заданной сети. Получающееся в результате минимальное порождающее дерево имеет суммарную длину 335.