

 |
 |

|
Промышленный лизинг
Методички
2-й шаг. Каждая из двух помеченных вершин графа порождает свою звезду. Рассмотрим все ребра этих звезд, за исключением тех, которые соединяют между собой уже помеченные вершины, выберем ребро наименьшей длины (если таких ребер несколько, выбираем любое из них) и пометим вершину, в которую входит это выбранное ребро. В результате выделенными оказываются два ребра графа, а помеченными уже три его вершины. Обозначим полученное дерево через . Ясно, что С . Если других вершин в графе нет, то искомое порождающее дерево построено и поставленная задача решена. В противном случае потребуется новый шаг. 3-й шаг. Каждая из трех помеченных вершин графа порождает свою звезду. Рассмотрим все ребра этих звезд, за исключением тех, которые соединяют между собой уже помеченные вершины, выберем ребро наименьшей длины (если таких ребер несколько, выбираем любое из них) и пометим вершину, в которую входит это выбранное ребро. В результате выделенными оказываются три ребра графа, а помеченными уже четыре его вершины. Обозначим полученное дерево через Т\ С % С Тъ. Если других вершин в графе нет, то искомое порождающее дерево построено и поставленная задача решена. В противном случае потребуется новый шаг. На каждом шаге и число выделенных ребер графа, и число помеченных вершин увеличиваются ровно на единицу. Тем самым, после п - 1-го шага количество выбранных ребер станет равным п - 1 и все п вершин графа окажутся помеченными. Обозначим полученное дерево через .£ ь ?CJ5C...CJC.i. Замечание. Первый шаг можно начинать с ребра наименьшей длины. Его легко найти путем простого перебора всех ребер графа. Если таких ребер несколько, выберем любое из них и пометим концы выбранного ребра. В результате две вершины графа окажутся помеченными. Если других вершин в графе нет, то искомое порождающее дерево построено и поставленная задача решена. В противном случае потребуется новый шаг, совпадающий со 2-м шагом алгоритма, предложенного выше [9]. Обоснование корректности алгоритма Обоснование корректности приведем для сети, в которой нет дуг равной длины (это условие кажется ограничительным лишь на первый взгляд; в реальных обстоятельствах длины разных отрезков проектируемой сети дорог хотя бы немного, но различаются). Итак, возьмем сеть с п узлами, обозначим через J* ее остов минимальной длины и покажем, что дерево Тп-и построенное описанным выше способом, непременно с ним совпадает* Априори возможны еще два случая: 1-й - дерево 3~ -1 целиком содержится в остове Г* (но, разумеется, не совпадает с ним Тп-{ * Г*) и 2-й - у дерева Tn i есть дуга, которой нет в остове Т*. Проведем рассуждения, исключающие оба эти случая. Случай 1-й. Если дерево Тп.х целиком лежит в остове Я8, то сумма длин всех его дуг оказывается меньше суммы всех дуг минимального остова Т*, что невозможно. Случай 2-й. Пусть а - дуга дереваТп ь не принадлежащая остовуТ*. По построению дерева i дуга а появляется на одном из шагов алгоритма. Предположим для определенности, что на к-м. Это означает, что у дерева Тк-{ ее еще нет, а у дерева Тк она уже есть. Напомним, как проводится к-й шаг. Приступая к нему, мы ищем дугу наименьшей длины, которая соединяла бы один из помеченных узлов дерева5-i с еще непомеченным на этот момент узлом исходной сети. Пусть это узлы А и В соответственно. Вследствие того, что остов Т* содержит все узлы исходной сети и связен, в нем существует путь, соединяющий узел А с узлом В и, конечно, отличный от дуги а. Перемещаясь по этому маршруту от помеченного узла А к непомеченному узлу В, мы непременно встретим дугу, один из концов которой уже помечен, а другой нет. Пусть это дуга Ь (рис. 9). Длина дуги Ъ должна быть больше длины дуги а (в силу ее выбора на к-м шаге). Заменив в минимальном остове J* дугу Ъ на дугу а, мы полу- 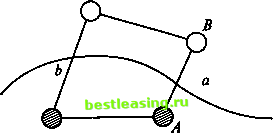 чим новый остов, сумма длин всех дуг которого окажется меньше, чем у остова X*, а это никак невозможно. 3.3. кратчайший маршрут Об этом алгоритме нужно заметить следующее: его труднее объяснить, чем научиться им пользоваться Лайтхилл [9], с. 335 Дана сеть, каждая дуга которой нагружена числом, равным его длине. Требуется найти кратчайший маршрут, ведущий от выделенного узла к каждому из других узлов сети. Алгоритм решения этой задачи, shortest-route algorithm, был предложен в 1959 году. Е. Дейкстрой [10]. Он представляет собой итерационную процедуру, в которой каждому узлу присваивается метка - либо постоянная и при этом показывающая расстояние от этого узла до выделенного (выделенный узел имеет постоянную метку), либо временная, где это расстояние оценивается сверху. В результате каждой итерации оценки уточняются, и ровно одна временная метка меняет свой статус на постоянную (после чего уже не меняется). Работу этого алгоритма удобно показать на конкретном примере. 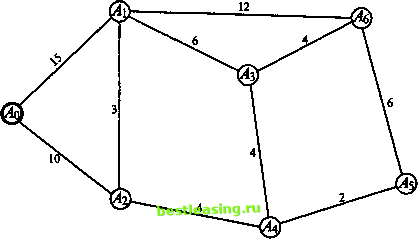
1 2 3 4 5 6 7 8 9 10 11 12 [ 13 ] 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 |