за которым будет следовать узел АкЕ%, а это означает, что дуга А,Ак £(%,%).

Можно сказать и по-другому: если из сети исключить все дуги какого-нибудь разреза, то в новой сети не останется ни одного ориентированного пути, связывающего источник Д> со стоком Ап. Поэтому разрез сети нередко называют разделяющим сечением.

Отсюда немедленно вытекает, что величину v произвольного потока <р не превышает пропускной способности С(Х, %) произвольного разреза (%,%):

v<C(%,%).

В сети, приведенной на рис. 23, множество % состоит из узлов Д> и Аъ множество % - из узлов Аи А3, А4пА5,а разрез (%,%) образуют дуги AqAu А2А3 и а2а4. Он имеет пропускную способность

7 + 2 + 2= 11.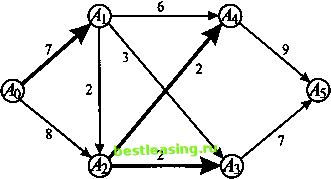

Рис. 23

Нетрудно убедиться в том, что пропускная способность любого другого разреза рассматриваемой сети превышает это число. Из последнего неравенства получаем, что

max v < min С(%, X),

(х,х)

где максимум берется по всем потокам <р в сети, а минимум - по всем ее разрезам (%,%).

В силу ограниченности пропускной способности транспортной сети всегда существует допускаемый ею поток (хотя и не обязательно один), величина которого максимальна. Такой поток наибольшей величины называют максимальным, maximal flow.

В свою очередь, разрез наименьшей пропускной способности называют минимальным.

Выписанное выше неравенство означает, что величина максимального потока не превосходит пропускной способности минимального разреза.

На самом деле справедливо более сильное утверждение.

ТЕОРЕМА. Для любой транспортной сети величина максимального потока из источника в сток совпадает с пропускной способностью минимального разреза.

Доказательство. В силу последнего неравенства достаточно показать, что существуют поток в сети и ее разрез такие, что величина этого потока и пропускная способность этого разреза равны.

Пусть <р - максимальный поток и v - его величина. Построим по нему разрез (%,%) так, чтобы были выполнены следующие условия:

1) сумма потоков по всем дугам разреза (Х9Х) совпадала с его пропускной способностью,

<р(Х9Х) = 2/p(Ai,Ak) = C(Xi%),

А,ex, AkSX

2) сумма потоков по всем дугам разреза (Х9Х) была равна нулю,

<р(Х,Х) = 2*,4) = 0.

А(ех, AkSX

Будем собирать узлы сети во множество X, начиная с источника Д> и действуя последовательно, шаг за шагом, по следующему правилу:

1) источник Ао Е X,

2) если узел AjGX и <p(Ah Ak) < c(Ah Ak)9 то Ak E X\ если узел At E X и <p(Ak, At) > О, то Ak E X.

По множеству узлов % мыразу же можем найти и множество узлов X. Покажем, что сток Ап GX.

Предположим противное - это не так и Ап §: X. Тогда из определения множества X вытекает, что существует путь из источника Д> в сток АЛ9 обладающий следующим свойством:

для всех его прямых дуг AtAk

<p(Ah Ak) < c(Ah Ak), а для всех его обратных дуг AkAf

<p(Aki Л) > 0.

Положим

a = mm(cik-<pik) (здесь минимум берется по всем прямым дугам этого пути),

(здесь минимум берется по всем обратным дугам этого пути) и

у = min(a, (5).

Ясно, что у > 0.

Тем самым, у нас появляется возможность изменить поток <р, увеличив его на у для всех прямых дуг нашего пути и уменьшив на у для всех его обратных дуг.

Нетрудно проверить, что в результате мы получим поток величиной v+y. Тем самым, исходный поток <р не максимален.

Полученное противоречие порождено сделанным нами предположением о том, что сток Ап £ X. Значит, это предположение неверно, и

Апех.

Таким образом, множество (Х,Х) есть разрез сети, разделяющий источник Ао и сток Ап.

Из самого построения множества X следует, что <p(Ah Ак) = c(Ah Ak) для любой дуги AfAk Е (Х9Х)9 <p(Aki At) = 0 для любой дуги AkAt Е (Х9Х) (в противном случае узел Ак входил бы во множество X). Это означает, что условия 1 и 2 на разрез (Х9Х) выполнены и его пропускная способность совпадает с величиной потока <р9

С(Х9Х) = v.

Но вернемся к примеру 1.

Согласно доказанной теореме, величина максимального потока в рассматриваемой сети должна быть равной 11. Нам же удалось найти поток лишь величиной 10. Это означает, что построенный полный поток не максимален и существует путь из источника Ао в сток АП9 для всех прямых дуг А{Ак которого

<р(А А < c(Ah Ак)9

а для всех его обратных дуг AkAt

<р(Ак, А,) > 0.

В рассматриваемом примере 1 это путь АоА2А\АуА5 (см. рис. 21а). Вычислим у. Имеем

у = min{5, 1, 3, 5} = 1.