Здесь совсем нелишне подчеркнуть, что такой же точки зрения придерживался и один из создателей линейного программирования Л.В. Канторович, о чем он и пишет в письме главному редактору журнала Management Science* P.M. Тралю в связи с опубликованием в Management Science* за 1960 год перевода своей работы Математические методы организации и планирования производства (Ленинград, 1939 г.) ([3], с. 375).

Исключив эти придуманные случаи, далее мы можем считать, что общая часть всех полуплоскостей в первой четверти представляет собой замкнутый выпуклый многоугольник со (рис. 6).

Рис. б

Заменив в выражении линейной функции w неизвестные х3, хп, через *i и х2, после приведения подобных получим

W = axxx +а2х2 + Ь,

где ах, а2 и Ъ - известные нам числа.

Линейная функция W непрерывна и достигает на ограниченном замкнутом множестве со наибольшего и наименьшего значений, но не во внутренней точке этого множества (не выполнено необходимое условие экстремума), а на его границе; более того, в одной из угловых точек (вершине многоугольника со).

Пусть, например, функция W достигает своего наибольшего (оптимального) значения в точке М*(х*,х*2) - вершине многоугольника су.

чения х3\ х* всех остальных неизвестных, по крайней мере два из которых равны нулю; для определенности, х * = 0 и х] = 0, к * /.

Важный вывод: оптимальное решение (если оно существует) всегда достигается в точке, где по меньшей мере два значения искомых неизвестных равны нулю.

Замечание. Возможен случай, когда наибольшего значения функция достигает не в одной точке, а на целом отрезке (стороне многоугольника со, включая его концы). Тогда оптимальное решение не единственно. Напомним, что мы рассматриваем случай, когда п - т = 2.

Сведем задачу о диете к общей задаче линейного программирования

и решим ее описанным выше способом.

Выберем в качестве свободных неизвестных х и у. Имеем

Из условий х > О, уО, w > О, v > О получаем треугольник ААВС (рис. 7). Вычислим координаты его вершин. Имеем

15х + 4у + и = 14, 150х+ 200>>- v= 300, jc > 0, у > 0, и > 0, v > О, w* = -150х - 250>> - max

w=-15x-4>>+ 14, v = 150x + 2(%- 300.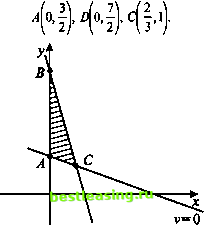

w=0 Рис. 7

Легко видеть, что При этом

х* =, / = 1, и * =0, v* =0. Из сказанного выше можно сделать

1-й оптимистичный вывод - так как искомое решение попадает в одну из вершин многоугольника и характеризуется тем, что по меньшей мере два из соответствующих значений неизвестных хь хп равны нулю, а число этих вершин конечно, то достаточно их просто все перебрать. Для этого можно поступить так:

1) выбрать пару свободных неизвестных,

2) положить их равными нулю,

3) вычислить соответствующие значения главных неизвестных,

4) отбросить случаи, когда хотя бы одно из них отрицательно,

5) вычислить значение целевой функции для всех оставшихся наборов (наборы, в которых значения всех главных неизвестных неотрицательны, называют опорными),

6) выбрать из найденных значений целевой функции наибольшее и получить оптимальный набор.

При л - /и = 3 число свободных неизвестных возрастает до трех, полуплоскости заменяются на полупространства, общей частью которых в первом октанте будет уже не выпуклый многоугольник, а выпуклый многогранник. Оптимальное решение будет достигаться в одной из его вершин и при этом по меньшей мере три из неизвестных хи х обратятся в нуль.

Картина, похожая на описанные выше, сохраняется и в случае, когда п - т > 3, а именно, оптимальное решение (если оно существует) всегда достигается на совокупности неизвестныххи хп, где по меньшей мере п - т из них обращаются в нуль.

Для простых задач, где число неизвестных невелико, нужное решение находится довольно быстро. К сожалению, множество задач линейного программирования, в которых все расчеты можно провести на руках, весьма мало, к тому же

решение задач линейного программирования вручную - труд крайне неприятный и изнурительный ([2], с. 70).

Несмотря на высказанное предостережение, сделаем еще один,

2-й оптимистичный вывод - поиск оптимального решения общей задачи линейного программирования можно осуществить путем