Однако есть более дешевое решение этой задачи

Его стоимость равна

300 1 + 400 1 + 200 3 + 200 3 + 300 7 = 4000.

Замечание. В последней схеме по самому дешевому маршруту ничего не перевозится, зато в полной мере задействован самый дорогой. И тем не менее общие затраты на перевозку оказались заметно меньше. Все дело в том, что решения, очевидные для двух маршрутов, не всегда оказываются выгодными для всей их совокупности. Тем самым, проблемы спроса и предложения не всегда подчиняются логике так называемого здравого смысла.

Итак, мы имеем следующую задачу линейного программирования:

т п

vv=EXc*x* *min

х.к = ап / = 1, 2, т;

к=\ т

х*=Ьк> к = 1>2, п, xik>0.

Отметим прежде всего, что все нетривиальные ограничения на искомые величины имеют вид равенств специального вида. Это обстоятельство позволяет отыскивать решение полученной системы линейных уравнений

2**=вм /=1> 2> >w

=Ьк, * = 1, 2, л,

простыми способами, один из которых мы опишем подробно.

Заметим, что общее число неизвестных в этой линейной системе равно т л, а число уравнений - т + л. Поэтому матрица системы имеет размеры (т + л) х (т п).

Совсем просто убедиться в том, что ранг этой матрицы всего на единицу меньше числа ее строк и равен т + п - 1. В силу сбалансированности задачи,

система совместна; число свободных неизвестных системы равно

к = тп - (т + п - 1) = (т - 1)(л - 1),

а число главных (базовых) - т + п- \.

Обращение в нуль к из неизвестных при неотрицательности остальных является необходимым условием того, что предъявленное решение системы является оптимальным. Необходимым, но не достаточным.

Любой такой набор неизвестных (в котором не более т + п - 1 неизвестных положительно, а остальные равны нулю) называют опорным.

Покажем на примере, как работает один из методов, называемый методом северо-западного угла, посредством которого можно найти опорный набор неизвестных в любой сбалансированной транспортной задаче.

Пример 2. Все условия представлены в таблице 1.

Таблица I

Начнем с левого верхнего (северо-западного) угла. Пункт В\ подал заявку на 48 единиц груза. Полностью исчерпав свои запасы (20 единиц), пункт А\ удовлетворяет ее лишь частично. Остальное добавляет пункт А2, также исчерпывая все свои запасы (23), и частично (5) пункт Л3,

48 = 20 + 23 + 5.

Последний полностью покрывает заявку пункта 1%. Оставшееся обеспечивается из запасов пункта Д.

Выпишем найденные значения соответствующих неизвестных. Имеем

*и = 20, х21 = 23, х31 = 5, х32 = 31, х33 =14, х43 =15, =17, х45 =10.

Их ровно восемь:

4 + 5-1,

остальные 12 неизвестных равны нулю (табл. 2 и рис. 9).

Таблица 2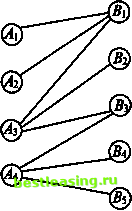

С Тем самым полученный набор является

опорным. Воспользуемся другим примером для того, чтобы показать, как, шаг за шагом улучшая опорные наборы, прийти к оптимальному. Пример 3. Все условия задачи представлены в таблице 3.