На отрезке JL целевая функция достигает максимума в целой точке L,

wL=17 (wy=12).

Условия на х и у в подзадаче аЪаЪ противоречивы.

Значение 17 целевой функции w = 5х + 6у в точке Ц1, 2) является наибольшим среди всех целых точек, подчиняющихся исходным условиям. Задача решена.

Действия, проведенные при поиске решения исходной задачи, удобно представить в виде дерева (дерева решения), на котором отражены основные этапы и последовательно получаемые результаты (рис. 45).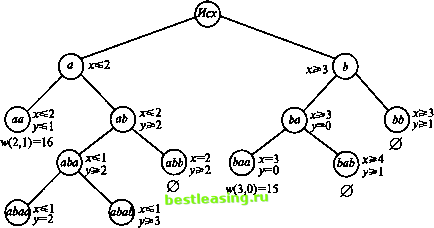

н<1,2)=17 0

Рис. 45

Замечание. Проходя еще раз по построенному дереву решения задачи целочисленного программирования, можно заметить, что в конечных вершинах (любого уровня) предъявляются либо целая точка, либо пустое множество.

4.4. литература

1. Фрейденталь Г. Математика как педагогическая задача: Книга для учителя. Ч. И. - М.: Просвещение, 1983.

2. Вентцель Е.С. Исследование операций. Задачи, принципы, методология. - М.: Дрофа, 2004.

4.4. Литература 125

3. Леонид Витальевич Канторович: человек и ученый: в 2 т. Т. 2. - Новосибирск: Изд-во СО РАН, филиал Гео , 2004.

4. Васильев Ф.П., Иваницкий А.Ю. Линейное программирование. - М.: Факториал Пресс, 2003.

5. Ашманов С А. Линейное программирование. - М.: Наука, 1981.

6. Стренг Г. Линейная алгебра и ее применения. - М.: Мир, 1980.

7. Вагнер Г. Основы исследования операций: в 3 т. - М.: Мир, 1972.

8. Зуховицкий СИ., Авдеева Л.Н Линейное и выпуклое программирование. - М.: Наука, 1964.

9. Rivett P. The craft of decision modeling. - John Wiley & Sons, 1994.

10. Моисеев КН. Математик задает вопросы... (Приглашение к диалогу). - М.: Знание, 1975.

11. Канторович Л.В., Горстко А.Б. Оптимальные решения в экономике. - М.: Наука, 1972.

Глава 5

ИГРЫ

... всякий открытый бой требует тайной подготовки, пусть малой и короткой по времени

([1], с. 364)

В практической деятельности нередко приходится рассматривать явления и ситуации, в которых участвуют две или более стороны, имеющие несовпадающие интересы и обладающие возможностями применять для достижения своих целей разнообразные действия. Подобные явления и ситуации принято называть конфликтными, или просто конфликтами.

Типичный конфликт характеризуется тремя основными составляющими: заинтересованными сторонами, возможными действиями этих сторон и их интересами.

Конфликтная ситуация, взятая из реальной жизни, как правило, довольно сложна. К тому же ее изучение затруднено наличием разных факторов, часть из которых не оказывает сколь-либо заметного влияния ни на развитие конфликта, ни на его исход. Поэтому, для того чтобы анализ конфликтной ситуации оказался возможным, необходимо отвлечение от этих второстепенных обстоятельств. При благоприятном развитии событий удается построить упрощенную, формализованную модель конфликта, которую принято называть игрой. От реальной конфликтной ситуации игра отличается еще и тем, что ведется по вполне определенным правилам.

Необходимость изучения и анализа конфликтов, представляемых в виде упрощенных математических моделей (игр), вызвала к жизни специальный математический аппарат - теорию игр.

Опишем основные понятия, используемые в этой теории.

Заинтересованные стороны называют игроками. Любое возможное для игрока действие (в рамках заданных правил игры)называется его стратегией. В условиях конфликта каждый игрок выбирает свою стратегию, в результате чего складывается набор стратегий, называемый ситуацией. Заинтересованность игроков в ситуации проявляется в том, что каждому игроку в каждой ситуации приписывается число, выражающее степень удовлетворения его интересов в этой ситуации и называемое его выигрышем в ней.