Смешанная стратегия второго игрока В, имеющего п чистых стратегий, описывается набором п неотрицательных чисел

qx £0, q2>0, qn>0, сумма которых равна 1,

Замечание. Каждая чистая стратегия является частным случаем смешанной стратегии. Чистая стратегия Af является смешанной стратегией, описываемой набором чисел ри Рг> > />л в котором

Pi = 1, Pj=0 О*0;

будем обозначать его 1,. А чистая стратегия Вк является смешанной стратегией, описываемой набором чисел qb q2, qn, в котором

Як=1 q,=0 (Ык)\

будем обозначать его Ц. Задав два набора

Р = (Л, Pi, ..> Рт)> Q = {, Яг, Яп)>

мы оказываемся в ситуации в смешанных стратегиях, которую коротко будем обозначать так - {Р, Q}.

Подчеркнем, что для соблюдения секретности каждый из игроков применяет свои стратегии независимо от другого игрока.

При этих условиях каждая обычная ситуация (в чистых стратегиях) {Ah Вк) является случайным событием и, ввиду независимости Р и Q, реализуется с вероятностью рдк.

Поэтому математическое ожидание выигрыша игрока А в смешанных стратегиях {Р, Q} будет равно

Это число и принимается за средний выигрыш игрока А в ситуации в смешанных стратегиях {Р, Q}.

Но вернемся к игре чет-нечет с 2 х 2-матрицей

[-! Л

и рассмотрим ее смешанное расширение. Выбирая стратегии игроков

Р = {/U-/>}, Q = {<7, 1-?}, вычислим средний выигрыш игрока А. Имеем

Я(р, ff)--- 0</><1, 0<<?<1.

Графиком этой функции является гиперболический параболоид, седловая точка которого имеет координаты (рис. 3)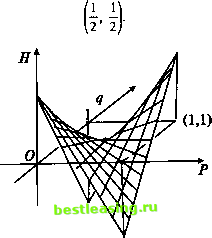

Рис. 3

Определение. Стратегии

P*={fl\ Л > Л.Ь Q* 92*. > Яп)

называются оптимальными смешанными стратегиями игроков А и В соответственно, если для любых стратегий Р и Q выполнено соотношение

Я(Р, Q)<#(P\ (П<Я(Р\ Q),

а ситуация {Р\ Q*} называется равновесной.

Выписанные неравенства можно пояснить так: стратегия Р* (стратегия Q*) оптимальна, если отклонение от нее игрока А (В) при условии, что игрок В (А) сохраняет свой выбор, приводит к тому, что средний выигрыш отклонившегося игрока не может увеличиться (а скорее уменьшится). Тем самым, получается, что если равновесная ситуация существует, то отклонение от нее невыгодно самому игроку.

Набор (Р*, Q*, v), состоящий из оптимальных смешанных стратегий Р* и Q* игроков А и В и значения игры

v=#(P\ Q*),

называется решением матричной игры в смешанных стратегиях.

Естественно, возникает первый ключевой вопрос: какие матричные игры имеют решение в смешанных стратегиях?

Ответ на него дает следующая основная теорема теории матричных

игр.

ТЕОРЕМА (Дж. фон Нейман) [2]. Для матричной игры с любой матрицей А величины

maxmin Я(Р, Q), пиптахЯ(Р, Q) существуют и равны между собой

maxmin Я(Р, Q) = min тахЯ(Р, Q). р Q Q р

Более того, существует хотя бы одна ситуация в смешанных стратегиях {Р*, Q*}, для которой выполняется соотношение

тахттЯ(Р, Q)= Я(Р\ Q*) = min тахЯ(Р, Q).

Замечание 1. Последнее равенство означает, что ситуация {P*,Q*} является равновесной, а набор (Р*, Q*, Я(Р*, Q*)) - оптимальным решением матричной игры.

Замечание 2. Экстремальные величины maxmin Я(Р, Q) и min тахЯ(Р, Q) всегда существуют вследствие того, что функция /$Р, tj) непрерывна на ограниченном замкнутом множестве

/=1 k=l

Для содержательного ответа на второй ключевой вопрос - как находить решение матричной игры, зная, что оно существует - необходимо сначала провести определенную подготовительную работу.

В предыдущих главах мы уже видели, что во многих задачах, где существование оптимального решения не вызывает никаких сомнений, его поиск нередко своеобразен и затруднителен. Искать оптимальное решение задачи, опираясь непосредственно на определение, сдержанно говоря, неразумно. Поэтому совершенно естественным выглядит желание сделать этот поиск как можно более простым и понятным.

Обоснование алгоритмов, посредством которых ищется оптимальное решение в смешанном расширении матричной игры, требует более глубокого проникновения в суть задачи и потому опирается на ряд не