Противоречивое соотношение возникло вследствие предположения о том, что для одной из положительных вероятностей (/?*) оптимальной

стратегии игрока А соответствующее значение его среднего выигрыша (#(1,. ,Q*)) меньше значения игры (v). Значит, это предположение не

верно, и для любой положительной вероятности из оптимального набора соответствующее значение среднего выигрыша игрока А равно значению игры.

Второе утверждение доказывается посредством аналогичных рассуждений.

Следствие. Пусть (Р*, Q*, v) - решение матричной игры в смешанных стратегиях. Тогда

из того, что H(lnQ*)<v, вытекает равенство р] = 0,

из того, что #(Р\ l*)>v, вытекает равенство =0.

В этом последнем скоплении равенств, по существу, и лежат истоки, питающие методы построения решений матричных игр. Опишем некоторые из них.

5.1.3. Методы решения матричных игр

Начнем с матричных игр, число стратегий хотя бы одного из игроков в которых равно двум.

Для построения решений 2 х л- и т х 2-игр существует эффективный метод, основанный на простых геометрических соображениях и, конечно, на доказанных выше утверждениях. Этот метод называют наглядно-графическим.

2 х л-игры

Пусть

п и - ахЛ

21 22 - а2п)

- матрица 2 х л-игры. Согласно следствию из теоремы 2

v = max min (а..р + а7. (1- р)).

Поэтому отыскание значения игры и оптимального значения р для игрока Л равносильно определению значения р, при котором функция

min(alkp + a2k(l-p)), (Ъ) достигает своего максимального значения, которое равно v.

Опишем общую схему решения этой задачи, приводящую к искомому результату.

Максимум функции (#) проще всего найти, построив ее график. Для этого поступим следующим образом.

Предположим, что игрок А выбрал смешанную стратегию Р = = {р, 1 -/>}, а игрок В - к-ю чистую стратегию Ц, к = 1, 2, п. Тогда средний выигрыш игрока А в ситуации {Р, \к) оказывается равным

(k):w = alkp + a2k(l-p).

На плоскости (р, w) это уравнение описывает прямую. Тем самым, каждой чистой стратегии игрока В будет соответствовать своя прямая.

Поэтому для построеия графика функции (#) сначала на плоскости (р, w) последовательно и аккуратно рисуются все прямые

(k):w = alkp + a2k(l-p)9 к = 19 2, п

(рис. 4). Затем для каждого значения р в полосе 0 р < 1 путем визуального сравнения соответствующих ему значений w на каждой из построенных прямых определяется и отмечается наименьшее (рис. 5).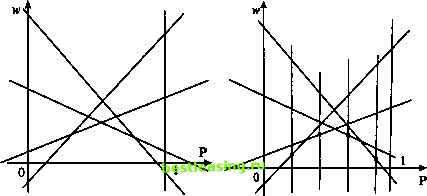

Рис. 4 Рис. 5

В результате описанной процедуры получается ломаная, которая и является графиком функции (#) (выделена жирным на рис. 6). В рассматриваемой полосе эта ломаная как бы огибает снизу все семейство построенных прямых, и по этой причине ее принято называть нижней огибающей.

Верхняя точка построенной нижней огибающей определяет и значение игры - v и оптимальную стратегию игрока А - Р* = {/>*, 1 - р*} (рис. 7).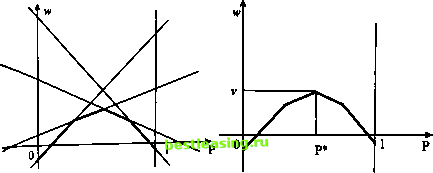

Рис. 6

Рис. 7

Опробуем описанную схему решения 2 х л-игры на конкретном примере.

Пример 4. Рассмотрим игру, заданную 2 х 6-матрицей

( 6 4 3 1 -1 0\ (-2 -1 1 0 5 4/

Решение.

1-й шаг. Анализ игры на наличие седловой точки. Нижнее значение игры равно -1, верхнее значение игры равно 1. Седловой точки нет. Решение игры нужно искать в смешанных стратегиях.

2-й шаг. Вычисление средних выигрышей игрока А (проводится при условии, что игрок В выбирает только чистые стратегии).

Из таблицы

6 4 3 1-10 -2-110 5 4

легко получаем

(1): и> = 6/>-2(1-/>), (2): w=4/>-(l-/>), (3): w = 3/> + (l-/>), (4): w=p, (5): w = -/> + 5(l-/>), (6): w= 4(1-/;).

3-й шаг. Построение нижней огибающей.