Аккуратно строим на координатной плоскости (р, w) все шесть прямых, уравнения которых получены на 2-м шаге (рис. 8), и находим нижнюю огибающую.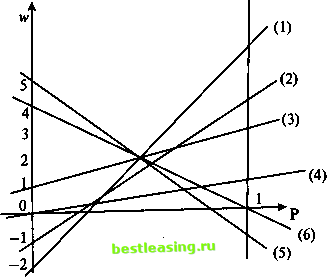

Рис. 8

Обращаем внимание читателя на то, что масштабы по осям р и w различны: в любой матричной игре ширина вертикальной полосы одна и та же (равна 1), в то время как w может принимать очень разные значения.

4-й шаг. Отыскание значения игры и оптимальной смешанной стратегии игрока А.

При аккуратном построении нижней огибающей нетрудно определить, точкой пересечения каких двух из построенных шести прямых является ее наивысшая точка. В данном случае это прямые (4) и (5), заданные уравнениями w =puw =-р + 5(1 - р) соответственно. Решая систему уравнений

w = р,

w = -/> + 5(l-/>),

получаем

5 .5

Рис. 9

Тем самым, значение игры v и оптимальная стратегия Р* игрока А найдены:

Собственно, этим и заканчивается решение игры для игрока А, поскольку его в первую очередь интересует отыскание собственной оптимальной стратегии и ожидаемого наилучшего гарантированного среднего результата.

Замечание. Решающий матричную игру обычно отождествляет себя с одним из игроков (как правило, это игрок А), считая другого своим противником. Это связано еще и с тем, что в некоторых случаях основное внимание уделяется поиску оптимальных стратегий только игрока Ау а стратегии противника могут вообще не интересовать исследователя.

Вместе с тем, в целом ряде случаев оказывается важным знать оптимальные смешанные стратегии обоих игроков.

Покажем теперь, как, зная оптимальную смешанную стратегию игрока А из примера 4, отыскать оптимальную смешанную стратегию игрока В и тем самым найти полное решение игры.

Прежде всего заметим, что для 1-й, 2-й, 3-й и 6-й чистых стратегий игрока В выполняются неравенства

(см. рис. 9).

Согласно следствию из теоремы 3, завершающему серию утверждений предыдущего раздела, сответствующие значения q * в искомой оптимальной смешанной стратегии

#(Р\ \k)>v *=1, 2, 3, 6

игрока J? должны быть равны нулю. Сказанное можно представить так:

Ях = 0, q\ =0, q\ = 0, q\ = q, q*s =1-?, q\ = 0

(из шести чистых стратегий игрока В выделены стратегии В4 и В5, соответствующие прямым (4) и (5), пересечение которых определяет наивысшую точку нижней огибающей).

Приравнивая любой из двух средних выигрышей игрока В (при условии, что игрок Л выбирает только чистые стратегии), отвечающий предложенной смешанной стратегии

0 0 0 q l-q 0

к значению игры

6 4 3 1 -10 -2-110 5 4

<7-(l-<7)=f, 5(1-?) = ,

(в обоих случаях) получаем, что

. 6

9 тт

Полное решение игры имеет следующий вид:

*-{f.f}. Q-{o,o,off,io}, v=.

В зависимости от формы нижней огибающей, может представиться несколько возможностей.

А. Нижняя огибающая имеет роено одну наивысшую точку (р*, w*).

1)0< <1ив наивысшей точке нижней огибающей пересекаются ровно две прямые. Тогда одна из этих прямых (fc-я) имеет положительный наклон, а другая (/-я) - отрицательный (рис. 10), и оптимальная смешанная стратегия игрока В получается, если положить

Я*к=Я> ?у=0, j*k, i*U

где q - решение уравнения

а1кЯ + аи(1~Я) = a2kq + a2t(l-tf).

2) 0 < />* < 1 и в наивысшей точке нижней огибающей пересекаются по меньшей мере три прямые. Выберем прямую с наибольшим положи-