Сравнивая полученные результаты с решением биматричной игры, можно заметить следующее:

если каждый игрок будет применять свои стратегии в этой игре, исходя только из матрицы своих выигрышей, то его оптимальный средний выигрыш совпадет с его выигрышем при равновесной ситуации; кстати, по своей матрице игрок может найти и оптимальную смешанную стратегию другого игрока (но не свою!).

Дилемма узников

Выигрыши игроков А и В описываются матрицами

ч з ч; 4

Проведем необходимые вычисления. Имеем

С= -1-(-9)-0 + (-6)= 2, а= -6-(-9)= 3, D= -1-0-(-9) + (-6)= 2, 0= -6-(-9)= 3.

Отсюда

Л (/>-1)(2<7-3) > 0, <*-1)<2/>-3) > О, pQq-З) > О, {П q(2p-3) > 0.

и, далее,

1°./> = 1, <7>, 2°./> = 0, д<, 3°.0</><1, <? = .

Rg = l, />>, 2*.д = 0, /><, 3*.0<д<1, />=.

Полученные зигзаги изображены на рис. 20.

Единственная равновесная ситуация - (0, 0). В этой ситуации каждый из игроков выбирает вторую чистую стратегию - сознаться - и теряет 6 лет.

Как мы уже отмечали ранее, отклонение от ситуации равновесия одного из игроков не дает ему никаких преимуществ. Однако при одновременном отклонении обоих каждый из них может получить больший выигрыш, нежели в равновесной ситуации. Например, в ситуации (1, 1), когда оба игрока выбирают первую чистую стратегию - молчать, - каждый из них теряет лишь 1 год.

Рис. 20

Напомним, что по условию задачи сговор (создание коалиции) между игроками недопустим.

Совершенно ясно, однако, что в рассматриваемых обстоятельствах ситуация (1,1) неустойчива - любой из узников, изменяя свою стратегию, увеличивает свой выигрыш (избегает наказания).

Покажем, как выглядят в рассматриваемой игре ситуации, оптимальные по Парето.

На единичном квадрате

0<р<1, 0<q<l

возможных значений вероятностей р и q заданы две функции

U=HA(p,q) = -pq-9p(l-q)-6(l-p)(l-q), V=HB(p,q) = -pq-9(l-p)q-6(l-p)(l-q).

Точки с координатами (U, V), вычисленными по приведенным формулам, на плоскости (U, V) заполняют четырехугольник с вершинами ЛГ (-1,-1), £(-9,0), М (-6,-6) и ЛГ(0,-9) (рис. 21). Граница Парето этого множества - ломаная NKL.

В качестве точки утопии здесь естественно рассматривать начальную точку 0(0,0). Идеальная точка JSf(-l,-l) - точка с наибольшими выигрышами для каждого из игроков - оказывается лучше, чем равновесная (рис. 22). Ей соответствуют чистые стратегии обоих игроков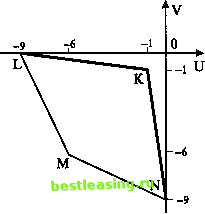

Рис. 21

Рис. 22

Семейный спор

Выигрыши игроков А и В в этой биматричной игре задаются так:

Но :) ч: °>

Проведя необходимые вычисления

С= 2-0-0 + 1 = 3, а= 1-0= 1, D= 1-0-0 + 2= 3, 0= 2-0= 2,

из неравенств

. (/>-1)(3?-0 £ 0, (q-l)(?p-2) 2> О, p(3q-l) а: О, Ю д(Ър-2) 2: О,

получаем, что

\°.р = \, q*1-, 2\р = 0)9<, 3°.0<р<1, q = j.

l:q = l, р>, 2 .? = 0, 3 .0<?<1, / .

Геометрически результат описывается так (рис. 23). Данная игра имеет три точки равновесия. Две из них отвечают чистым стратегиям игроков,