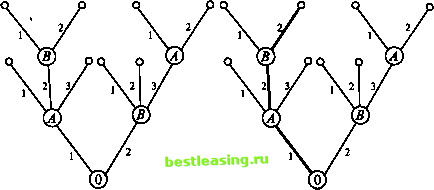Рис. 24 Рис. 25

случайным механизмом (иногда его называют природой). Например, в позиционной игре, представленной на рисунке 24 своим деревом, первый ход производится случайно.

Пользуясь графическим описанием игры, можно сказать, что процесс игры состоит в переходе от начальной позиции к окончательной через непосредственно следующие одна за другой промежуточные позиции.

Каждая окончательная вершина определяет единственную последовательность идущих друг за другом звеньев, которая связывает начальную вершину с данной (рис. 25). Такая цепь называется партией.

Число различных партий равно числу окончательных вершин (позиций).

Мы будем рассматривать здесь только антагонистические позиционные игры: в каждой окончательной позиции задан числовой выигрыш игрока А (а выигрыш игрока В ему противоположен).

В шахматах функция выигрышей игрока Л (белых) определяется так:

+1 на выигрываемых партиях,

0 на ничейных партиях,

-1 на проигрываемых партиях.

Функция выигрышей игрока В (черных) отличается от функции выигрышей белых только знаком.

Различают позиционные игры с полной информацией и позиционные игры с неполной информацией.

В позиционных играх с полной информацией (пример - шашки, шахматы) каждый игрок при своем ходе знает ту позицию дерева игры, в которой он находится.

В позиционных играх с неполной информацией игроку при своем ходе позиция дерева игры, в которой он фактически находится, точно неизвестна. Этот игрок знает лишь множество позиций, включающее

в себя его фактическую позицию. Такое множество позиций называется информационным множеством.

В игре с неполной информацией игрок при своем очередном ходе знает, в каком информационном множестве он находится, но ему неизвестно, в какой именно позиции этого множества.

Позиции, принадлежащие одному и тому же информационному множеству, объединяются (например, посредством пунктирных линий) (рис. 26).

Рассмотрим примеры игр, состоящих из двух ходов, которые последовательно делают участвующие в них игроки А и В.

Начинает игрок А: он выбирает одну из двух возможных альтернатив - число х, равное либо 1 (первая альтернатива), либо 2 (вторая альтернатива). На ход игрока Л игрок В отвечает своим ходом, выбирая одну из двух возможных альтернатив - число у, равное либо 1 (первая альтернатива), либо 2 (вторая альтернатива).

И в результате игрок А получает вознаграждение или вынужден платить штраф.

Замечание. Альтернативы, из которых делают выбор игроки, вообще говоря, не совпадают; числа 1 и 2 - это просто номера альтернатив. Пример 1.

1-й ход. Игрок А выбирает число х из множества двух чисел {1,2}. 2-й ход. Игрок В выбирает число у из множества двух чисел {1,2}, зная выбор числа х игроком А.

Функция W(x, у) выплат игроку А за счет игрока В задается так:

(1,1) = 1, (2,1) = -2, (1,2) = -1, W(2,2) = 2.

На рис. 27 показаны дерево игры и информационные множества.

Пример 2. Пусть выполнены все условия предыдущего примера, кроме одного - хода игрока В.

2-й ход - игрок В выбирает число у из множества двух чисел {1,2}, не зная выбора числа х игроком А. В этом случае информационные множества выглядят так, как показано на рис. 28.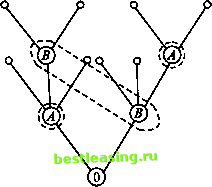

1-1-2 2 1-1-2 2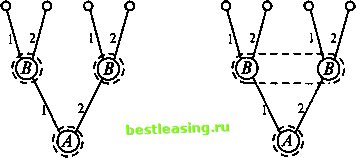

Рис. 27 Рис. 28

5.3.2. Нормализация позиционной игры

Заранее определенную последовательность ходов игрока, выбранную им в зависимости от информации о ходах другого игрока и ходах игрока О (природы), будем называть чистой стратегией этого игрока.

В том случае, если в игре нет случайных ходов (игрок О в игре не участвует), выбор игроком А и игроком В чистых стратегий однозначно определяет исход игры - приводит к окончательной позиции, где игроки А и В и получают свои выигрыши.

Это обстоятельство позволяет сводить позиционную игру к матричной игре. Сам процесс сведения позиционной игры к матричной называют нормализацией позиционной игры.

Покажем на нескольких примерах, как это делается.

Пример 3. Опишем стратегии игроков из примера 1. Стратегию игрока А можно задать числом х, показывающим, какую альтернативу, первую или вторую, выбрал этот игрок. Тем самым, у игрока А две чистых стратегии:

Ai - выбрать х = 1, А2 - выбрать х = 2. Стратегию игрока В, приняв во внимание, что выбор игрока Л на 1-м ходе ему известен, удобно описать упорядоченной парой

Здесь yi Cvi = 1,2) - альтернатива, выбираемая игроком В при условии, что игрок Л выбрал первую альтернативу, х = 1, ay2 (у2 = 1,2) - альтернатива, выбираемая игроком В при условии, что игрок Л выбрал вторую альтернативу, х = 2.

Например, выбор игроком В стратегии [2, 1] означает, что если на 1-м ходе игрок А выбрал х = 1, то игрок В на своем ходе должен выбрать