у = 2. Если же на 1-м ходе игрок А выбрал х = 2, то согласно этой стратегии игрок В на своем ходе должен выбрать у = 1.

Таким образом, у игрока В четыре чистых стратегии:

В\ - [1, 1], у = 1 при любом выборе х;

В2 - [1, 2], у = х при любом выборе х;

1?з - [2, 1], >> * х при любом выборе х;

В4 - [2, 2], >> = 2 при любом выборе х.

Покажем теперь, как рассчитать выигрыши игрока А.

Пусть, например, игрок А выбрал стратегию Ах - (1), а игрок В - стратегию В2 - [1, 2]. Тогда х = 1, а из стратегии [1, 2] вытекает, что у = 1. Отсюда

Ж(х,;у)=Ж(1,1) = 1.

Подобным образом рассчитываются и остальные выигрыши игрока А.

Результаты расчетов записываются обычно или в виде таблицы выигрышей игрока А

или в виде матрицы

где, как обычно, строки соответствуют стратегиям игрока А, а столбцы - стратегиям игрока В.

Нетрудно заметить, что полученная матрица имеет седловую точку. Оптимальные стратегии игроков: Ах - (1), и В3 - [2,1]. Тем самым, игрок А на 1-м ходе выбирает х = 1, а игрок В на 2-м ходе выбирает у = 2. Значение игры v = - 1.

Пример 4. Опишем стратегии игроков из примера 2.

У игрока А они те же, что и в предыдущем примере:

А{ - выбрать х = 1, А2 - выбрать х = 2.

Так как игроку В выбор игрока А неизвестен, то есть игрок В не знает, в какой именно из двух позиций он находится (см. рис. 28), то у него те же две стратегии:

В\ - выбрать у = 1, В2 - выбрать у = 2.

Соответствующие таблица выигрышей игрока А и матрица игры имеют следующий вид:

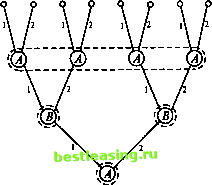
1 -1

Полученная матрица седловой точки не имеет. Оптимальные смешанные стратегии игроков: Р={2/3, 1/3} и Q={l/2, 1/2}. Значение игры v = 0.

Замечание 1. На этих двух примерах хорошо видно, что результат сведения позиционной игры к матричной напрямую зависит от степени осведомленности игроков. В частности, отсутствие у игрока В сведений о выборе, сделанном игроком А, приводит к уменьшению количества его возможных стратегий. Кроме того, сравнивая ответы, полученные в примерах 3 и 4, нетрудно заметить, что снижение уровня осведомленности игрока (в данном случае игрока В) делает для него исход игры менее благоприятным.

Замечание 2. Приведенные выше примеры всех возможных вариантов не исчерпывают даже в этом, самом простом, случае двухходовых позиционных игр.

Перейдем к позиционным играм, состоящим из трех ходов, и рассмотрим несколько примеров сведения их к матричным играм, сосредоточив основное внимание на одном из наиболее ответственных шагов нормализации - описании стратегий игроков.

Пример 5.

1-й ход делает игрок А: он выбирает число х из множества двух чисел {1,2}.

2-й ход делает игрок R зная выбранное игроком А число х, он выбирает число у из множества двух чисел {1,2}.

3-й ход делает игрок А: не зная о выбранном игроком В числе у на 2-м ходе и забыв выбранное им самим на 1-м ходе число х, он выбирает число z из множества двух чисел {1,2}.

После этого игрок А получает вознаграждение W(x, у9 z) за счет игрока В, например, такое

W(1,U) = W(l,l,2) = W(l,2,l) = W(l,2,2) =

-2, 4, 1,

W(2,U) = W(2,l,2) = IV (2,2,1) = IV (2,2,2) =

3, 0, -3, 5.

На рис. 29 показаны дерево игры и информационные множества. Нормализуем эту игру.

Поскольку игроку В выбор игрока А на 1-м ходе известен, то у игрока В те же четыре стратегии, что и в примере 2:

Вх - [1,1], В2 - [1,2], В3 - [2, 1], ВА - [2, 2].

Игрок А на 3-м ходе не знает предыдущих выборов - ни значения х, ни значения у. Поэтому каждая его стратегия состоит просто из пары чисел (х, z), где х (х = 1, 2) - альтернатива, выбираемая игроком А на 1-м ходе, a z (z = 1,2) - альтернатива, выбираемая игроком А на 3-м ходе.

Например, выбор игроком А стратегии (2,1) означает, что на 1-м ходе он выбирает х = 2, а на 3-м ходе - z = 1.

Таким образом, у игрока А тоже четыре стратегии:

Аг - (1, 1), А2 - (1, 2), Л3 - (2, 1), Л - (2, 2).

Покажем теперь, как рассчитываются выигрыши игрока А в этой игре.

Пусть, например, игрок А выбрал стратегию А2, (1, 2), а игрок 5 - стратегию В3, [2, 1].

Из того, что х = 1, вытекает, что >> = 2. Значение г = 2 выбрано игроком А независимо от выбора игрока В. Вычисляя значение функции выигрышей для набора х = I, у = 2 к z = 2, получаем

mx,y,z)= Щ1,2, 2) = -4.

Посредством подобных рассуждений определяем и остальные пятнадцать выигрышей. Это позволяет построить таблицу выигрышей игрока А. Имеем