5.4. Некоторые другие виды игр

Мы можем пройти через многие и многие группы игр. И увидеть, как сходства то появляются, то снова исчезают.

Л. Витгенштейн

Реальные конфликтные ситуации приводят к различным видам игр. Выше мы достаточно подробно остановились на трех из них - матричных, биматричных и позиционных играх.

В этом разделе нам хотелось бы обратить внимание читателя на удивительное разнообразие конфликтных ситуаций, которые удается формализовать до состояния математической игры. Мы опишем эти ситуации с разной степенью подробности, заметив, что в перечне книг, сопровождающем эту главу, указаны и те, в которых показано, какими средствами и как именно достигается их разрешение.

5.4.1. Неантагонистические позиционные игры

В предыдущем разделе мы достаточно подробно остановились на позиционных играх двух лиц, где интересы одного из игроков (игрока А) полностью определяли интересы другого (игрока В) - они были противоположны интересам игрока А Вместе с тем нередко оказывается, что интересы игроков различаются не в столь резкой форме.

Приведем два простых примера.

Пример 1.

1-й ход. Игрок А выбирает число х из множества {1, 2}. 2-й ход. Игрок В выбирает число у из множества {1,2}, зная выбор числа х игроком А.

Функции выплат игрокам А и В - WA(x, у) и Wb(x, у) - задаются так:

WA(l, 1) = 1, WA(l, 2) = -1, WA(2, 1) = -2, WA(2, 2) = 2,

И1, 1) = 2, WAX, 2) = 1, W& 1) = 1, W& 2) = 2.

Дерево игры показано на рис. 37.

Исход игры зависит от того, каковы намерения игрока В - максимизировать свой выигрыш

Wx, у) -+ max,

максимизировать свой относительный выигрыш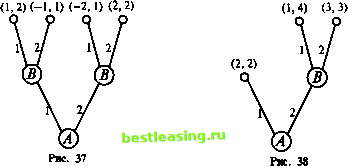

В первом случае это достигается при х = 1 и у = 1: JVB(l, 1) = 2(WA(1, 1) = 1); при х = 2 и у = 2: И(2, 2) = 2((2, 2) = 2).

Во втором случае при х = 2 и у = 1: И2, 1) - (W(2, 1) = 1 - (-2) = 3.

Пример 2.

Игра задается деревом (рис. 38).

1-й ход. Игрок А выбирает число х из множества {1, 2}.

Если х = 1, то каждый из игроков получает свой выигрыш, равный 2.

Если jc = 2, то право 2-го хода получает игрок В9 где он и выбирает число у из множества {1, 2}.

При у = 1 выигрыш игрока А равен 1, а игрока 5 - 4. При >> = 2 оба игрока получают поровну - по 3.

В случае, когда каждый из игроков стремится к получению максимального выигрыша и любые виды кооперации запрещены, исход игры ясен - игрок А выбирает х = 1, и игра заканчивается.

Заметим, что при х = 2 и у = 2 каждый из игроков получает по 3 (такой исход предпочтительней простейшего (1,1)), и, если допустить соглашение между игроками, это обстоятельство вполне может изменить исход игры.

5.4.2. Игры на единичном квадрате (борьба за рынки)

Одна из конкурирующих фирм (игрок А) пытается вытеснить другую фирму (игрок В) с одного из двух рынков сбыта. Предположим, что общая сумма средств, выделенная на это игроком А9 равна 1. Типичной стратегией игрока А является разделение выделенной суммы на две части: х (О < х < 1) для первого рынка и 1 - х для второго. Подобным обра-

зом выглядят и стратегии игрока Вт. выделение им части у (О £ у £ 1) своей суммы на первый рынок и 1 - у на второй.

Будем считать, что если игрок А добился превосходства на одном из рынков (на другом превосходства автоматически добивается игрок В), то он вытесняет противника с этого рынка и получает выигрыш, пропорциональный избытку вложенных средств с коэффициентом, характеризующим важность рынка (этот коэффициент равен к{ для первого рынка и к2 для второго). Тогда функция выигрыша #(х, у) игрока А определяется формулой

кх-у), 0£y<x£l, О, х = у,

Ясно, что функция выигрыша игрока В равна -#(х, у). 5.4.3. Игры типа дуэли

Два дуэлянта (игроки А и В) начинают сходиться в момент времени t=0. У каждого пистолет заряжен одной пулей. Они встретятся в момент времени t = 1 (если только ни один из них не поразит другого раньше). Каждый из дуэлянтов может выстрелить, когда пожелает. Если при этом одному из них удастся поразить противника, а самому остаться невредимым, то он становится победителем (его выигрыш равен 1) и дуэль тут же прекращается. Если оба промахнутся, дуэль заканчивается вничью (выигрыш каждого из игроков равен 0). Если оба выстрелят одновременно и каждый поразит противника, то дуэль также считается окончившейся вничью.

Будем считать, что меткость выстрелов при сближении игроков возрастает таким образом, что если какой-либо игрок выстрелит в момент времени f, то вероятность поражения противника будет равна t

Обозначим момент выстрела игрока А через х, а момент выстрела игрока В через у.

Различают два вида дуэлей: бесшумную (когда игроки не слышат выстрелов друг друга) и шумную (когда игроки слышат выстрелы).

Бесшумная дуэль. При х < у вероятность попадания игрока А равна х, а промаха 1-х. Это означает, что вероятность его поражения игроком В равна (1 - х)у. Тем самым, функция выигрыша игрока А при х < у будет иметь вид

Я(х,у) = (+1)х + (-1)(1-х)у = х-у + ду. Рассуждая аналогично, при х>у получим