#(х, >;) = (- 1)у + (+1)(1 - у)х = х - у - ху. При х = у имеем

Шумная дуэль. При х < д> вероятность выигрыша игрока Л равна х, а проигрыша 1 - х (если игроке промахнулся и, следовательно, не может больше выстрелить, игрок В будет увеличивать свои шансы на успех, ожидая, пока у не сравняется с 1). Поэтому при х < у функция выигрыша игрока А будет иметь вид

#(x,;v) = (+l)x + (-l)(l-x) = 2x-l. Рассуждая аналогично, при х > у получим

Я(х,у)-(-1)у + (+1)а-у)-1-2>г. При х = у имеем

Ясно, что в обоих случаях функции выигрыша игрока В будут противоположны выписанным.

5.4.4 Иерархические игры

Опишем несколько ситуаций, которые сводятся к играм двух лиц, в которых игроки, прежде чем выбрать свои стратегии, обмениваются сведениями о своих выборах. Такого рода игры описывают взаимодействия между верхним и нижним звеньями управления (начальником и подчиненным, центром и производителем продукции и т. п.) и называются иерархическими. Будем считать, что первый игрок осуществляет управление вторым игроком и делает сообщение первым.

Ситуация 1-я. Первый игрок (центр) сообщает второму игроку (производителю продукции) цену на продукцию. Второй игрок, зная цену, выпускает продукцию в определенном количестве.

Ситуация 2-я. Первый игрок (центр) перед выбором имеет полную информацию о возможностях второго игрока (производителя продукции) и сообщает ему величину премии, обещаемую за произведенную продукцию.

Ситуация 3-я. Первый игрок (центр) указывает величину ресурса, которую он выделяет второму игроку (производителю продукции), когда тот сообщает ему свои производственные возможности.

Подробный разбор описанных ситуаций содержится в [7] (с. 103).

5.4.5. Игры дележа

Обратимся к играм, в которых игроки делят общий выигрыш (денежный доход). Такие игры называют кооперативными, или играми дележа. В этих играх (в отличие от рассмотренных выше) число участников может быть любым (но, разумеется, конечным).

В кооперативной теории нет единого понятия разумного дележа. Более того, различные соображения оптимальности могут приводить к разным множествам разумных дележей.

Здесь мы изложим один из возможных подходов к разрешению поставленной проблемы.

Пусть § - множество из п игроков:

Любое подмножество Р С § будем называть коалицией.

Сопоставляя каждой коалиции Я ее выигрыш (доход) г<Я), мы определяем на множестве всех коалиций характеристическую функцию v.

Ясно, что таких, характеристических, функций на одном и том же множестве коалиций может быть задано много. Мы ограничимся рассмотрением характеристических функций, для которых неравенство

v(P)+v(§)z v(PU§) (*)

выполняется для любых двух непересекающихся коалиций Я и §.

Это означает, что если у двух коалиций Я и § нет общего игрока, то сумма их выигрышей не превосходит выигрыша коалиции, их объединяющей.

Из неравенства (#) вытекает, что для любых непересекающихся коалиций Яь Рт выполняется неравенство

Jv()<v$), /=i

откуда, в частности, следует, что разбиения множества § на коалиции, при котором их суммарный гарантированный выигрыш превосходил бы выигрыш всех игроков, не существует.

В задаче - джаз-оркестр (см. главу 2, задача восемнадцатая) множество игроков состоит из трех человек, а характеристическая функция принимает следующие значения:

v(g.) = 200, v(g2)=300, v(g3) = 0, v(g.,g2) = 800, v(g2,g3) = 650, v(g1,g3) = 500, v(g.,g2,g3) = 1000.

Непосредственной проверкой легко убедиться в том, что для этой характеристической функции v условие (ir) выполнено.

Замечание. Если бы условие (#) нарушалось (как это происходит, скажем, при v(gi) = 400), то собрать трио музыкантов за 1000$ было бы затруднительно, если только к совместной игре их не толкали иные стимулы.

В приводимом ниже примере характеристическая функция задана не столь явно.

Пример. Рассмотрим две пары матриц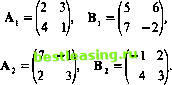

Первый игрок выбирает номер строки /, второй - номер столбца к, а третий - номер пары гЕ {1, 2}. Выигрыш первого игрока равен агл,

второго - а третьего - сг& =10-я-6£.

Сумма выигрышей всех трех игроков в этой игре постоянна и равна 10.

Найдем !<&).

Первый игрок играет против коалиции {g2, &} в игру с матрицей

Вычеркивая первый и второй столбцы и решая получившуюся в результате 2 х 2-игру

находим, что v(ft) = 5/3. Отсюда v(g2, ft) = Ю - 5/3 = 25/3.

Несложно найти значения характеристической функции и для других коалиций:

v(g2) = 1, v(gj, g3) = 9, v(g3) = 4, v(g g2) = 6. Введем важное понятие дележа.

Определение. Дележом называется любой набор у = (уи Уп)> подчиненный условиям