Метод уступок - лицо, принимающее решения (руководитель), подводится к выбору решения путем постепенного ослабления первоначальных требований, как правило, одновременно невыполнимых.

Метод идеальной точки - в области допустимых значений неизвестных ищется такая их совокупность, которая способна обеспечить набор значений критериев, в том или ином смысле ближайший к наилучшему, как правило, недосягаемому (в так называемой точке утопии).

Метод свертывания - лицо, принимающее решения (руководитель), сводит многокритериальную задачу к задаче с одним критерием.

Метод ограничений - множество допустимых значений неизвестных уменьшается путем осмысленного введения дополнительных ограничений на заданные критерии.

Метод анализа иерархий - на основании суждений экспертов оценивается вклад в общую оценку каждого критерия.

Хотя перечисленные методы и носят отчетливо выраженный количественный характер, они нередко позволяют прояснить интересующую нас качественную картину.

Следует признать, что применение этих методов в реальных ситуациях, когда как число подлежащих определению величин и охватывающих их ограничений, так и число самих критериев особенно велики, сопряжено со значительными объемами вычислений. Поэтому при рассмотрении серьезной проблемы без привлечения современных вычислительных средств и эффективных алгоритмов никак не обойтись.

Накопленный опыт преподавания в университете, обсуждение с математически неискушенными слушателями указанных выше и иных методов дает нам основание сказать, что суть метода и алгоритм, его реализующий, удобнее всего раскрывать, опираясь не столько на теоретические рассуждения (разумеется, за многими из используемых подходов стоит серьезное теоретическое обоснование), сколько показывая, как именно надлежит действовать в конкретной ситуации (пусть даже и сравнительно простой).

Обращаясь к многокритериальным задачам, мы сталкиваемся с ситуацией, когда оптимальность искомого решения уже не столь очевидна, как это было ранее. Поэтому возникает необходимость в выборе еще одного, нового критерия, критерия оптимальности, и предъявлении заслуживающих внимания обоснований и достаточно веских доводов в его пользу.

Не имея возможности сколь-либо подробно останавливаться на возможностях каждого из перечисленных выше методов, мы опишем здесь лишь их малую часть, ограничившись в основном линейными задачами,

то есть такими, в которых используются только линейные функции и линейные ограничения (уравнения и неравенства).

Мы сознательно ограничиваемся анализом задач, в которых число неизвестных величин равно двум. Это даст нам возможность показать основные идеи наглядно (при помощи рисунков). Что же до количества критериев, то мы рассмотрим конкретные примеры сначала с двумя, а затем и с тремя критериями.

6.1. Множество Парето

Рассмотрим на плоскости (77, V) произ- ук вольное множество Я (рис. 1). Каждая точка плоскости обладает одним из следующих трех свойств:

либо все точки, ближайшие к ней, принадлежат множеству Я (такая точка называется внутренней точкой множества

либо все точки, ближайшие к ней, множеству Q не принадлежат (такая точка называется внешней точкой по отношению к множеству Я),

либо сколь угодно близко от нее расположены как точки множества Я, так и точки, множеству Я не принадлежащие (такие точки называются граничными точками множества Я).

Множество всех граничных точек множества называется его грани-

цей.

Обозначение: дЯ.

Граничная точка может как принадлежать множеству Я, так и не принадлежать. В дальнейшем мы будем рассматривать только такие множества, которым принадлежат все точки их границы.

Пусть М - произвольная точка множества Я, внутренняя или граничная, и (7и К- ее координаты. Поставим следующий вопрос: можно ли, оставаясь во множестве Я, переместиться из точки Мв близкую точку так, чтобы при этом одновременно увеличились обе координаты.

Если М- внутренняя точка множества Я, то это бесспорно возможно (рис. 2а).

Если же М - граничная точка множества Я, то такое возможно не всегда. Например, путем перемещения точек М{ и М2 в другие точки множества Я можно одновременно увеличить обе координаты каждой из них (рис. 26). Однако перемещая точку М3 по вертикальному отрезку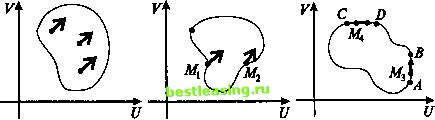

Рис. 2а

Рис. 26

Рис. 2в

АВ вверх (рис. 2в), мы увеличиваем лишь координату V (координата С/при этом остается неизменной). Перемещая точку МА горизонтального отрезка CD вправо, мы увеличиваем координату U(при этом координата сохраняет свое значение). Что же касается точек дуги BD, то, стремясь увеличить одну из координат, мы непременно уменьшаем другую. Иными словами, на дуге BD лежат точки, одновременного увеличения обеих координат которых можно достичь лишь выйдя из множества Я (рис. 2г). Во множестве Я, изображенном на рисунке 3 и состоящем из 11 точек, этим свойством обладает каждая из четырех выделенных черных точек.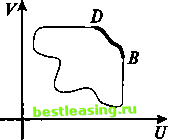

Рис. 2г

Рис. 3

Тем самым, точки множества Я можно разбить на три класса: к первому классу относятся точки, которые, оставаясь во множестве Я, можно сдвинуть так, чтобы одновременно увеличились обе координаты (в этот класс попадают все внутренние точки множества Я и часть его граничных точек),

второй класс образуют граничные точки, перемещением которых по множеству дЯ можно увеличить только одну из координат при сохранении значения второй (вертикальный отрезок АВ и горизонтальный отрезок CD на границе множества Я),