

 |
 |

|
Промышленный лизинг
Методички
о (Фтах> тах)  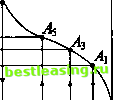 Ф2 Ф4Ф6 Ф5 Фз *1 Рис. 9 1-й шаг, 1-я уступка. Лицо, принимающее решения, соглашается немного ослабить свои изначальные требования по 1-му критерию и заменить Фтах на Фь Аналитик-специалист при помощи границы Парето множества Я (дуги АВ) показывает ему, что соответствующее значение 2-го критерия не может быть больше Ч. Скорее всего лицо, принимающее решения, не сочтет полученную пару (Фь Ч) приемлемой, но согласится немного ослабить свои требования на значение 2-го критерия, что приведет к необходимости 2-го шага. 2-й шаг, 2-я уступка. Лицо, принимающее решения, соглашается заменить Wmax на Аналитик-специалист при помощи границы Парето множества Я (дуги АВ) показывает ему, что соответствующее значение 1-го критерия не может быть больше Ф2. Скорее всего лицо, принимающее решения, не сочтет полученную пару (Ф2, *Рг) приемлемой, но согласится еще немного (по сравнению с Фх) ослабить свои требования по 1-му критерию, что приведет к необходимости 3-го шага. Ясно, что с каждым шагом, с каждой уступкой просматриваемая часть границы Парето будет сокращаться (см. рис. 9) и, когда пара (Фя, Ч?п)9 полученная на п-м шаге, покажется лицу, принимающему решения, приемлемой, процесс поиска подойдет к концу. Останется лишь найти решение системы ABDAlBDAlB2 ЭА3В2 ЭА3В4 ЭА5ВА D... Ф(х,) = ФЛ, Щх,у) = Ча. Полученная в результате пара чисел х = х* и у = у* и будет ответом к исходной задаче, полученным методом уступок. 6.3. Метод идеальной точки Другой подход, также использующий множество Парето, называется методом идеальной точки. Он состоит в отыскании на границе Парето точки, ближайшей к точке утопии, задаваемой лицом, принимающим решения. Как уже отмечалось выше, обычно лицо, принимающее решения, формулирует цель в виде желаемых значений показателей, и часто в качестве координат целевой точки выбирается сочетание наилучших значений обоих критериев (как правило, эта точка при заданных ограничениях не достигается; поэтому ее и называют точкой утопии). Рассмотрим конкретный пример поиска идеальной точки. Пример. Пусть на множестве со плоскости (х, у), определяемом системой неравенств 0<х<2, 0<д><2, заданы две линейные функции tf=5x->>+2, ( К = -х + Зд> + 2. Требуется найти решение задачи U max V max при условии, что (х, у) Е О). Множество со представляет собой квадрат (рис. 10), вершины которого имеют координаты 0,0), 5(0,2), 0(2,2), Д2,0). В силу линейности критериев U и V квадрат ABCD переходит в параллелограмм PQRS (рис. 11), координаты вершин которого Л2,2), 0,8), Д(10,6), 5(12,0) вычисляются по формулам (-&). 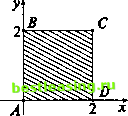 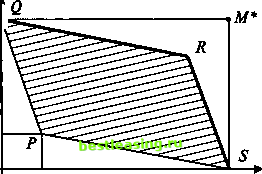 12 U Рис. 11 Точка утопии М*(12, 8) считается заданной (ее координаты суть наибольшие значения U и V). Граница Парето параллелограмма PQRS состоит из двух отрезков - QR и RS (рис. 12). Точка, ближайшая к точке утопии М*, принадлежит множеству Парето и должна лежать на одном из составляющих его отрезков - или на отрезке QR, или на отрезке RS. Рис. 12 Чтобы найти на отрезке QR точку, ближайшую к точке М*, воспользуемся прямой, проходящей через точки Q и А Подставляя в общее уравнение прямой aU+pV=y координаты точек Q и R, 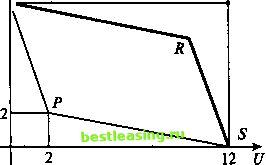
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 [ 75 ] 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 |