returns. In contrast, the autocorrelation patterns for the absolute returns are strikingly regular. Consider the series for the DM-$ exchange rate in Fig. 4a. The strong intraday pattern induces a distorted U-shape in the sample correlogram 19. Notice also how the size of the autocorrelations at the daily frequencies decay slowly over the first four days, only to increase slightly at the fifth, or weekly, frequency. This signals the presence of a minor day-of-the-week effect, which we ignore in the remainder. Fig. 4b for the S&P 500 futures returns is equally telling. The slowly declining U-shape occupies exactly 80 intervals, corresponding to the daily frequency.

3.2. Interpretation in terms of a suggestive intraday return model

The pronounced systematic fluctuations in the return correlogram provide an initial indication that direct ARCH modeling of the intraday return volatility would be hazardous. Standard ARCH models imply a geometric decay in the return autocorrelation structure and simply cannot accommodate strong regular cyclical patterns of the sort displayed in Fig. 4. Instead, it seems intuitively clear that the combination of recurring cycles at the daily frequency and a slow decay in the average autocorrelations may be explained by the joint presence of the pronounced intraday periodicity documented above coupled with the strong daily conditional heteroskedasticity 20. The following stylized model provides a simple specification of the interaction between these two components,

n I N

R,= ZR n = o-t-iZs ztn. (l)

n=l П /1=1

Here, R, denotes the daily continuously compounded return calculated from the /V uncorrected intraday return components, Rt n. The conditional volatility factor for day t is denoted by cr(, while sn refers to a deterministic intraday periodic component and Z, и is an i.i.d. mean zero, unit variance error term assumed to be independent of the daily volatility process, {cr,}. Both volatility components must be non-negative i.e. cr, > 0 a.s. for all t and sn > 0 for all n. The following terminology for the normalized, deterministic sample means and covariances for the periodic structure will prove convenient:

if>M(,) = l, rj: = Af(и,.). -LS2n=M(s2),

7V n=l /Vn=l n=l

where sn+jN = sn for any integer j and 0 < n < N.

19 A corresponding figure is presented by Dacorogna et al. (1993). However, in their analysis the correlations at the daily frequencies are sharply diminished due to a strong weekend effect. By excluding weekend returns we have effectively eliminated this distortion.

20 The temporal variation in daily financial market volatility have been successfully modeled by ARCH type processes (see Bollerslev et al. (1992) for a survey of this extensive literature).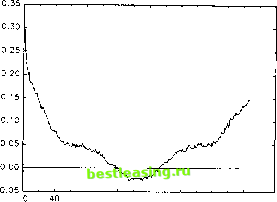

120 160 200 240 280 320 Five Minute Lag

0.35

Five Days Correlogram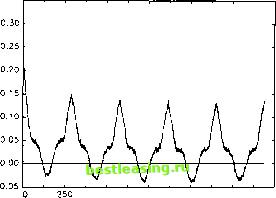

500 750 1000 1250 Five Minute Lag

Fig. 4. Intraday absolute returns, (a) DM-$, (b) S&P 500.

1500

In the absence of intraday periodicity (sn = 1 for all n) the daily returns may be represented in the form Rt = <TlN~i/2Y.n=]NZln, where the return component Л? 1/2Е = hNZln is i.i.d. with mean zero and unit variance. Thus, Eq. (1) extends the standard volatility model for daily returns to an intraday setting with independent return innovations and deterministic volatility patterns. Of course, this type of periodicity is annihilated when the returns are measured at the daily frequency. In particular, letting Z, denote an i.i.d. random variable with E(Z,) = 0 and Var(Z,) = 1, we have

Rt = M]/2(s2)o-tZn

0.30 I

0.00

-0.05 I-i-1-1-1-i-1-1-1--1-.-1-.-1-.-1

0 10 20 30 40 50 60 70 80 Five Minute Lag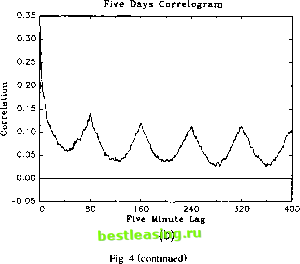

so that the expected absolute return equals M]/2(s2)a[E\Zt\. Since Mx/2(s2) > 1, the expected daily absolute return is an increasing function of the fluctuations in the intraday periodic pattern. However, this effect is limited to a scale factor. Letting с = (E\Z,\)~2 - 1 > 0, it follows that for t=tr,

Covlcr 01)

i - -vhJ;,-)- <3)

Hence, the presence of periodic components reduces the overall level of the