WHY DO THE DEGREES HAVE TO BE EVEN?

Showing that an Eulerian path exists only when the degrees on all nodes are even (except at most two) rests on a simple observation. This observation is about paths in the graph. Consider one path through the bridges:

A - C - B --C -D

The edges being used are:

AC1 - BC1 - BC2 - CD

The edges connecting the intermediate nodes in the path come in pairs. That is, there is an outgoing edge for every incoming edge. For instance, node C has four edges visiting it, and node B has two. Since the edges come in pairs, each intermediate node has an even number of edges in the path. Since an Eulerian path contains all edges in the graph and visits all the nodes, such a path exists only when all the nodes in the graph (minus the two end nodes) can serve as intermediate nodes for the path. This is another way of saying that the degree of those nodes is even.

Euler also showed that the opposite is true. When all the nodes in a graph (save at most two) have an even degree, then an Eulerian path exists. This proof is a bit more complicated, but the idea is rather simple. To construct an Eulerian path, start at any node (even one with an odd degree) and move to any other connected node which has an even degree. Remove the edge just traversed from the graph and make it the first edge in the Eulerian path. Now, the problem is to find an Eulerian path starting at the second node in the graph. By keeping track of the degrees of the nodes, it is possible to construct such a path when there are at most two nodes whose degree is odd.

Euler devised a solution based on the number of edges going into or out of each node in the graph. The number of such edges is called the degree of a node. For instance, in the graph representing the seven bridges of Konigsberg, the nodes representing the shores both have a degree of three-corresponding to the fact that there are three bridges connecting each shore to the islands. The other two nodes, representing the islands, have degrees of 5 and 3. Euler showed that an Eulerian path exists only when the degrees of all the nodes in a graph are even, except at most two (see technical aside). So, there is no way to walk over the seven bridges of Konigsberg without traversing a bridge more than once, since there are four nodes whose degrees are odd.

Traveling Salesman Problem

A more recent problem in graph theory is the Traveling Salesman Problem. In this problem, a salesman needs to visit customers in a set of cities. He plans on flying to one of the cities, renting a car, visiting the customer there, then driving to each of other cities to visit each of the rest of his customers. He

leaves the car in the last city and flies home. There are many possible routes that the salesman can take. What route minimizes the total distance that he travels while still allowing him to visit each city exactly one time?

The Traveling Salesman Problem is easily reformulated using graphs, since graphs are a natural representation of cities connected by roads. In the graph representing this problem, the nodes are cities and each edge has a weight corresponding to the distance between the two cities connected by the edge. The Traveling Salesman Problem therefore is asking: What is the shortest path that visits all the nodes in a graph exactly one time? Notice that this problem is different from the Seven Bridges of Konigsberg. We are not interested in simply finding a path that visits all nodes exactly once, but of all possible paths we want the shortest one. Notice that all Eulerian paths have exactly the same length, since they contain exactly the same edges. Asking for the shortest Eulerian path does not make sense.

Solving the Traveling Salesman Problem for three or four cities is not difficult. The most complicated graph with four nodes is a completely connected graph where every node in the graph is connected to every other node. In this graph, 24 different paths visit each node exactly once. To count the number of paths, start at any of nodes (there are four possibilities), then go to any of the other three remaining ones, then to any of the other two, and finally to the last node (4 * 3 * 2 * 1 = 4! = 24). A completely connected graph with n nodes has n! (n factorial) distinct paths that contain all nodes. Each path has a slightly different collection of edges, so their lengths are usually different. Since listing the 24 possible paths is not that hard, finding the shortest path is not particularly difficult for this simple case.

The problem of finding the shortest path connecting nodes was first investigated by the Irish mathematician Sir William Rowan Hamilton. His study of minimizing energy in physical systems led him to investigate minimizing energy in certain discrete systems that he represented as graphs. In honor of him, a path that visits all nodes in a graph exactly once is called a Hamiltonian path.

The Traveling Salesman Problem is difficult to solve. Any solution must consider all of the possible paths through the graph in order to determine which one is the shortest. The number of paths in a completely connected graph grows very fast-as a factorial. What is true for completely connected graphs is true for graphs in general: The number of possible paths visiting all the nodes grows like an exponential function of the number of nodes (although there are a few simple graphs where this is not true). So, as the number of cities increases, the effort required to find the shortest path grows exponentially. Adding just one more city (with associated roads) can result in a solution that takes twice as long-or more-to find.

This lack of scalability is so important that mathematicians have given it a name: NP-where NP means that all known algorithms used to solve the problem scale exponentially-not like a polynomial. These problems are considered difficult. In fact, the Traveling Salesman Problem is so difficult that it is used for evaluating parallel computers and exotic computing methods-such as using DNA or the mysteries of quantum physics as the basis of computers instead of the more familiar computer chips made of silicon.

All of this graph theory aside, there are pretty good heuristic algorithms for computers that provide reasonable solutions to the Traveling Salesman Problem. The resulting paths are relatively short paths, although they are not guaranteed to be as short as the shortest possible one. This is a useful fact if you have a similar problem. One common algorithm is the greedy algorithm: start the path with the shortest edge in the graph, then lengthen the path with the shortest edge available at either end that visits a new node. The resulting path is generally pretty short, although not necessarily the shortest (see Figure 10.6).

Often it is better to use an algorithm that yields good, but not perfect results, instead of trying to analyze the difficulty of arriving at the ideal solution or giving up because there is no guarantee of finding an optimal solution. As Voltaire remarked, Le mieux est Iennemi du bien. (The best is the enemy of the good.)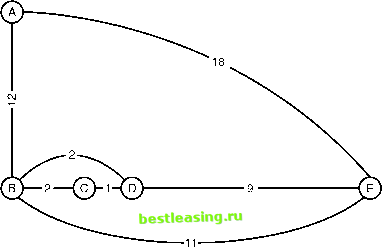

Figure 10.6 In this graph, the shortest path (ABCDE) has a length of 24, but the greedy algorithm finds a much longer path (CDBEA).