using the market model is 0.965%. Sinccthe standard error of the one-day good-news average abnormal return is 0.104%, the value ot J\ is 9.28 and the null hypothesis that the event has no impact is strongly rejected. The story is the same for the bad-news firms. The event day sample abnormal return is -0.679%, with a standard error of 0.098%, leading to J\ equal to -6.93 and again strong evidence against the null hypothesis. As would be expected, the abnormal return of the no-news firms is small at -0.091% and, with a standard error of 0.098%, is less than one standard error from zero. There is also some evidence of the announcement effect on day one. The average abnormal returns arc 0.251% and -0.204% for the good-news and the bad-news firms respectively. Both these values are more than two standard errors from zero. The source of these day-one effects is likely to be that some of the earnings announcements arc made on event day zero after the close of the stock market. In these cases the effects will be captured in the return on day one.

The conclusions using the abnormal returns from the constant-mean-rcturn model arc consistent with those from the market model. However, there is some loss of precision using the constant-mcan-return model, as the variance-of the average abnormal return increases for all three categories. When measuring abnormal returns with the constant-mean-rcturn model the standard errors increase from 0.104% to 0.130% for good-news firms, Ггот 0.098% to 0.124% for no-news firms, and from 0.098% to 0.131% forVl>ad-news firms. These increases are to be expected when considering a sample of large firms such as those in the Dow Index since these stocks tend to have an important market component whose variability is eliminated using the market model.

The CAR plots show that to some extent the market gradually learns about the forthcoming announcement. The average CAR of the good-news firms gradually drifts up in days -20 to -1, and the average CAR of the bad-news firms gradually drifts down over this period. In the days after the announcement the CAR is relatively stable, as would be expected, although there docs lend to be a slight (but statistically insignificant) increase for the bad news firms in days two through eight.

4.4.6 Inferences with Clustering

In analyzing aggregated abnormal returns, we have thus far assumed that the abnormal returns on individual securities arc uncorrelated in the cross section. This will generally he a reasonable assumption if the event windows of tf e included securities do not overlap in calendar time. The assumption allows us to calculate the variance of the aggregated sample cumulative abnormal returns without concern about covariances between individual sample CARs, since they arc zero. However, when the event windows do

overlap, the covariances between the abnormal returns may differ from zero, and the distributional results presented for the aggregated abnormal returns arc not applicable. Bernard (1987) discusses some of the problems related to clustering.

When there is one event date in calendar time, clustering can he accommodated in two different ways. First, the abnormal returns can be aggregated into a portfolio dated using event time, and the security level analysis of Section 4.4 can be applied to the portfolio. This approach allows for cross correlation of the abnormal returns.

A second way to handle clustering is to analyze the abnormal returns without aggregation. One can test the null hypothesis that the event has no impact using unaggregated sccurity-by-security data. The basic approach is an application of a multivariate regression model with dummy variables for the event date; it is closely related to the multivariate /-test of the CAPM presented in Chapter 5. The approach is developed in the papers of Schipper and Thompson (1983, 1985), Malatesta and Thompson (1985), and Collins and Dent (1984). It has some advantages relative to the portfolio approach. First, it can accommodate an alternative hypothesis where some of the firms have positive abnormal returns and some of the firms have negative abnormal returns. Second, il can handle cases where there is partial clustering, that is, where the event date is not the same across linns but there is overlap in the event windows. This approach also has some drawbacks, however. In many cases the test statislic has poor finite-sample properties, and often il has little power against economically reasonable alternatives.

4.5 Modifying the Null Hypothesis

Thus far we have focused on a single null hypothesis-that the given event has no impact on the behavior of security returns. With this null hypothesis either a mean effect or a variance effect represents a violation. However, in some applications wc may be interested in testing only for a mean effect. In these cases, we need to expand the null hypothesis to allow for changing (usually increasing) variances.

To accomplish this, we need to eliminate any reliance on past returns in estimating the variance of the aggregated cumulative abnormal returns. Instead, we use the cross section of cumulative abnormal returns to form an estimator of the variance. Boeluner, Musumeci, and Potilsen (1991) discuss this methodology, which is best applied using the constant-mean-rcturn model to measure the abnormal return.

The cross-sectional approach to estimating the variance can be applied to both the average cumulative abnormal return (CAR(T, ti)) and the average standardized cumulative abnormal return (SCAR(T. r2)) . Using the

cross section lo form estimators of (Ik* variances \vc have

I v

Va.fCARlr r-.) = Y,(iAri>r~CATix-i))t (4.f .l)

j -V

Var[SCAR(r,. r..)] = - £(SCAR,(t ts) - S0AR(t tj))S. (4.5.2)

For these estimators of the variances to he consistent we require the abnormal returns lo he uncoi related in the cross section. An absence of clustering is siiIIn ient for this requirement. Note that cross-sectional ho-moskedaslicil) is not required for consistency. (liven these variance estimators, the null hypothesis that the cumulative abnormal returns are zero can then be tested using large sample theory given the consistent estimators of the variances in (4.5.2) and (4.5.1).

One may also be interested in the impact of an event on the risk of a (inn. The relevant measure of risk must be defined before this issue can be addressed. One choice as a risk measure is the market-model beta as implied by the Capital Asset Pricing Model. Given this choice, the market model can be formulated to allow die beta to change over the event window and the stability of the beta can be examined. See Kane and Unal (1988) for an application of this idea.

4.6 Analysis of Power

To interpret an event study, we need to know what is our ability to detect the presence of a nonzero abnormal return. In this section we ask what is the likelihood that an event-study lest rejects the null hypothesis for a given level of abnormal return associated with an event, thai is, we evaluate the power of the (est.

We consider a two-sided test of the null hypothesis using the cuinulativc-abnornial-reiui n-based statistic /, from (4.4.22). We assume that the abnormal returns are uncorrelated across securities; thus the variance of CAR is <7-(n, г.), where о-(r(, r->) = l/AV- ff,-(ri, r-j) and N is the sample size. Under the null hypothesis die distribution of J\ is standard normal. For a two-sided test of size i* we reject the null hypothesis if ]\ < Ф~(0/2) or if

/i > Ф (I -u/2) where Ф(-) is the standard normal cumulative distribution

function (CDF).

Given an alternative hypothesis Нл and the CDF of J\ for this hypothesis, we can tabulate the power of a test of size a using

Р(аМл) = Pr(y, < Ф~() I HA)

+ Prfj, > ф-O-f) I Нд). I (4.6.1)

With this framework in place, we need to posit specific alternative hypotheses. Alternatives are constructed to be consistent with even studies using data sampled at a daily interval. We build eight alternative hypotheses using four levels of abnormal returns, 0.5%, 1.0%, 1.5%, and 2.0%, and two levels Tor the average variance of the cumulative abnormal return ofja given security over the sampling interval, 0.0004 and 0.0016. These variances correspond to standard deviations of 2% and 4%, respectively. The sample size, that is the number of securities for which the event occurs, is varied from 1 to 200. We document the power for a test with a size of 5% (a = 0.05) giving values of -1.96 and 1.96 for Ф 1 (a/2) and Ф~1 (1 - a/2), respectively. In applications, of course, the power of the test should be considered when selecting the size.

The power results-are presented in Table 4.2 and are plotted in Figures 4.3a and 4.3b. The results in the left panel of Table 4.2 and in Figure 4.3a are for the case where the average variance is 0.0004, corresponding to a standard deviation of 2%. This is an appropriate value for an event which does not lead to increased variance and can be examined using a one-day event window. Such a case is likely to give the event-study methodology its highest power. The results illustrate that when the abnormal return is only 0.5% the power can be low. For example, with a sample size of 20 the power of a 5% test is only 0.20. One needs a sample of over 60 firms before the power reaches 0.50. However, for a given sample size, increases in power are substantial when the abnormal return is larger. For example, when the abnormal return is 2.0% the power of a 5% test with 20 firms is almost 1.00 with a value of 0.99. The general results for a variance of 0.0004 is that when the abnormal return is larger than 1% the power is quite high even for small sample sizes. When the abnormal return is small a larger sample size is necessary to achieve high power.

In the right panel of Table 4.2 and in Figure 4.3b the power results are presented for the case where the average variance of the cumulative abnormal return is 0.0016, corresponding to a standard deviation of 4%. This case corresponds roughly to either a multi-day event window or to a опеч1ау event window with the event leading to increased variance which is accommodated as part of the null hypothesis. Here we see a dramatic decline in the power of a 5% test. When the CAR is 0.5% the power is only 0.09 with 20 firms and only 0.42 with a sample of 200 firms. This magnitude

Tayle 4.2. Power of event-study If si statistic J\ to reject Ihe null hy/wlhesis that the abnoi mat return is zero.

observations included in the study, and a is the stmare mot of the average variance of the abnormal return across firms.

of abnormal return is difficult to detect with the larger variance of 0.0010. In contrast, when the CAR is as large as 1.5% or 2.0% the 5% lest still has reasonable power. For example, when the abnormal return is 1.5% and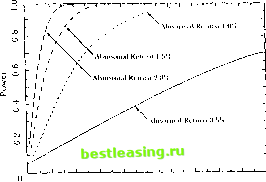

10 20 30 40 5(1 60 70 0 90 100 Sample Si/.e (a)

0 1() 20 3(1 40 5(1 60 70 HO 90 100 Sample Size

Figure 4.3. Power of Event-Study Test Statistic /, to lirjeel the Null Hypothesis that the Abnormal Return Is /em, Wlien the Square Root of the Average Variance of the Abnormal Return Acmss Pinns is (a) 2% and (b) 4%

there is a sample size of 30, the power is 0.54. Cent-rally if the abnormal return is large one will have little difficulty rejecting the null hypothesis of no abnormal return.

Wc have calculated power analytically using distributional assumptions. If these distributional assumptions are inappropriate then our power calculations may be inaccurate. However, Brown and Warner (1985) explore this