Построение графика ограничений

Процедура построения графика ограничений проста:

1. Заменить знаки неравенства знаком равенства. Это преобразовывает ограничение в уравнение прямой линии.

2. Определить место пересечения построенной линии с осями координат.

а. Чтобы найти, где линия пересекает ось Х2, приравняем xi = О и решаем уравнение для значения Х2.

б. Чтобы найти, где прямая пересекает ось xi, приравняем Х2 = О и решаем уравнение для значения xi.

3. Отметить точки пересечения на осях и соединить их прямыми. (Обратите внимание: если ограничение содержит только одну переменную, это будет вертикальная линия на графике для переменной xi, или горизонтальная линия для переменной Х2.)

4. Указать штриховкой (или стрелками на концах линии ограничений) направление неравенства: больше или меньше. (Общее правило для определения области, удовлетворяющей неравенству: выбрать точку с координатами (0,0) и посмотреть, больше она или меньше, чем значение ограничения.)

5. Повторить пункты 1-4 для каждого ограничения.

Сначала выстроим ограничение по машинному времени: xi -ь 3 Х2 < 12.

1. Запишем это как равенство: xi -ь 3 Х2 = 12.

2. Приравняем xi = О и решим для Х2 :

(0) -ь 3 Х2 = 12, следовательно Х2 = 4. Приравняем Х2 = О и решим для х):

XI -ь 3 (0) - 12, следовательно xi = 12.

3. Отметим точки на графике и соединим их прямой.

4. Заштрихуем область, которая удовлетворяет ограничению. (Подстановка Х1= О, Х2=0 в уравнение даст значение, равное О, которое меньше 12. Следовательно, все точки с этой стороны линии имеют значения меньше 12.) Смотрите рис. 5п-1. Обратите внимание, что только площадь в первом секторе заштрихована, учитывая ограничение неотрицательности.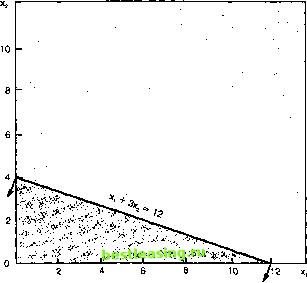

Рис. 5п-1. Ограничение по машинному времени

Зторое ограничение выстраивается сходным образом:

1. Запишем его в виде равенства: 4 xi + 3 Х2 = 24.

2. Приравняем xi = О и решим для хг:

4(0) + 3 Х2 = 24, получим Х2 = 8. Приравняем Х2 = О и решим для xi: 4 XI + 3 (0) = 24, получим х] = 6.

3. Отметим эти точки на графике и соединим прямой линией.

4. Заштрихуем площадь, удовлетворяющую ограничению (см. рис. 5п-2). Обратите внимание, что некоторые точки отвечают только одному ограничению, а другие точки удовлетворяют обоим.

Определение области возможных решений

Область возможных решений - это совокупность всех точек (т.е. площадь), которая удовлетворяет всем ограничениям. (Вспомним, что оси xj и Х2 образуют ограничение неотрицательности.) Заштрихованная площадь на рис. 5п-2-это область возможных решений для нашей задачи.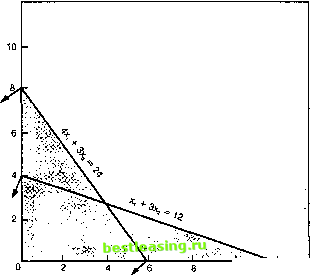

10 /12

Рис. 5п-2. На график наносится ограничение по сырью

Построение графика целевой функции

Целевая функция-это фактически семейство линий. Эти линии параллельны, но каждая из них представляет различное значение. Например, одна линия может быть 4xi + 5x2 = 20, другая 4xi +5 Х2= 40, а третья 4xi + 5x2= 60. Эти линии показаны на рис. 5п-3. Обратите внимание, что линии параллельны и что линия, более удаленная от начала координат, соответствует большему значению целевой функции. Крометого, каждая линия-линия одинаковой прибыли: каждая комбинация xi и Х2 на линии будет давать ту же самую прибыль (например, $40).

М ожно построить большое количество различных линий, которые могут быть использованы при решении. Некоторые из этих линий будут пересекать область возможных решений, а некоторые- нет. Это важно, потому что точки, лежащие за пределами области возможных решений, не могут быть оптимальными решениями проблемы. Из трех показанных на рис. 5п-3 линий только одна линия 4 Х] + 5 Х2 = 20 имеет точки, лежащие в пределах области возможных решений. Однако нетрудно увидеть, что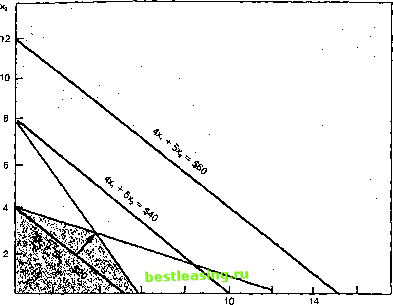

0 2 4 6 8

Рис. 5п-3. Три линии одинаковой прибыли

можно провести и другие линии, параллельные данной, но расположенные дальше от начала координат. Нам нужна последняя линия, которая только касается области возможных решений, потому что она будет соответствовать самому большому осуществимому значению целевой функции.

Вместо использования метода проб и ошибок мы легко можем подобрать линию, которая будет соответствовать максимальной прибыли для комбинации Xj и Х2 в области возможных решений. Все что нам для этого нужно-линия одинаковой прибыли, которая пересекает эту область.

Выберите значение для построения целевой функции. Одно из самых удобных значений - произведение коэффициентов у переменных Xj и Х2 (в нашем случае это 4 и 5: 4 X 5 =20). Это одна из линий, представленных на рис. 5п-3. Обратите внимание, что она пересекает область возможных решений. Однако так бывает не всегда. Когда линия проходит за пределами области возможных решений, разделите выбранное значение целевой функции (например, 60) на константу, таким образом, чтобы после этого линия проходила через область возможных решений (например, 60:3 = 20, пересечение имеет место). Напротив, если линия пересекает область возможных решений, но слишком близко к началу координат (т.е. она бесполезна), надо умножить ее значение на константу-1,5,2,10,100 или др., - чтобы получить более полезную линию.

Постройте линию так, как построили линию ограничения: установите Xj = О и найдите решение относительно Х2, затем установите Х2 = О и найдите решение относительно Xj.

Так как прибыль увеличивается по мере удаления линии от начала координат, сдвигайте линию параллельно себе самой (представьте ряд параллельно проведенных линий). Цель состоит в том, чтобы найти самую дальнюю точку в области возможных решений, которой касается одна из параллельных линий. Координаты точки Xj и Х2 показывают количество Xj и Х2, которое максимизирует целевую функцию (см. рис. 5п-4). В данном примере это та точка, где пересекаются два ограничения.

Хотя в некоторых случаях можно считать это непосредственно с графика, обычно для определения точных координат пересечения используют алгебраические методы. Это можно осуществить путем одновременного решения уравнений двух линий (т.е.находят одно значение xj и одно значение Х2, которые будут удовлетворять обоим равенствам). Для этого, сначала запишем оба равенства ограничений: