Целевая функция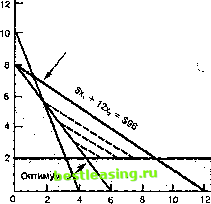

Рис. 5п-8. Оптимум находится в последней точке соприкосновения линии целевой функции, когда она перемещается в направлении начала координат

Недостаток и избыток

Связывающее ограниче-

ние - ограничение, которое формирует оптимальную угловую точку области возможных решений.

штттштттшшшштшшвтжш

Недостаток - когда оптимальные значения переменных решения подставляю юя в ограничение типа S и результирующая величина меньше, чем величина пра-I вой части.

Если ограничение формирует угловую точку оптимума в области возможных решений, то оно называется связывающим ограничением (binding constraint).

В действительности, оно ограничивает значение целевой функции; если ограничение будет слабее (менее жестким), то возможно улучшение решения. Для ограничения, которое не является связывающим, ослабление ограничения не окажет действия на решение.

Если подставить оптимальные значения переменных в левую часть связывающего ограничения, результирующее значение будет точно равно значению правой части ограничения. Однако в случае с необязательным ограничением будет иметь место различие. Если левая часть больше, чем правая, то говорят, что имеется избыгок; если левая часть меньше правой, то имеется недостаток. Недостаток может возникать только в ограничении типа <; это та величина, на которую левая часть меньше правой, когда оптимальные значения переменных подставляются в левую часть.

Избыток может возникать только в ограничениях типа >; это величина, на которую левая часть больше

правой, когда оптимальные значения переменных подставляются в левую часть.

Например, предположим, что оптимальные значения для модели: xj = 10 и Х2 = 20. Одно из ограничений имеет вид:

3x1 +2x2 < 100

Подставляя оптимальные значения в левую часть, получим: 3(10)+ 2(20) =70

Так как ограничение имеет тип < различие между значениями 100 и 70 (т.е.ЗО) - это недостаток. Предположим, что оптимальные значения xj = 20 и Х2 = 20. Подстановка этих значений в левую часть ограничения даст 3(20) + 2(20) = 100. Т.к. левая и правая части равны (недостаток равен 0), имеет место связывающее ограничение.

Избыток - когда оптималь- ные значения переменных решения подставляются в ог- раничение типа > и результи- 1 рующая величина больше, чем величина правой части. 1

Теперь рассмотрим ограничение: 4Х1+Х250

Предположим, что оптимальные значения Xj = 10 и Х2 = 15; подставляя их в левую часть, получим: 4(10)+ 15=55

Так как это ограничение типа >, разность между левой и правой частями является избытком. Если оптимальные значения были xj = 12 и Х2 = 2, то в результате подстановки левая часть будет равна 50. Следовательно, ограничение будет связывающим, а излишка не будет (т.е. излишек равен 0).

Симплексный метод

Симплекс - алгоритм ли- ш нейного программирования, с помощью которого можно I решать задачи, содержащие более двух переменных.

Симплексный метод - универсальный алгоритм линейного программирования, который широко используется для решения крупномасштабных задач. Хотя ему недостает простоты и наглядности графического подхода, его способность решать задачи с более чем 2 переменными делает его чрезвычайно ценным для решения многих проблем управления производством. Симплексная методика включает ряд итераций (повторов); проводятся последовательные усовершенствования, до тех пор пока не будет достигнуто оптимальное решение. Методика его требует лишь простых математических операций (сложение, вычитание, умножение и деление), но вычисления длинны и утомительны, и малейшая ошибка может привести к большим погрешностям. По этой причине, большинство пользователей данной методики полагаются на компьютеры, чтобы производить вычисления, в то время как сами концентрируются на решении. Все же, определенное знакомство с ручными вычислениями полезно для понимании симплексного процесса. Вы обнаружите, что лучше не использовать ваш калькулятор в работе над решением этих задач, потому что округление может легко исказить результаты. Поэтому лучше работать с дробными числами.

Хотя симплекс может легко обрабатывать три или более переменных, вы лучше поймете его методику на примере задачи с двумя переменными, потому что сможете сравнивать симплексные вычисления с графическим решением данной задачи.

Давайте рассмотрим симплексное решение для той же самой задачи, которая использовалась для иллюстрации графического метода. Повторим постановку задачи: Максимизировать: Z = 4 Xj + 5x2 Ограничения: Xj + 3x2 < 12

4xi+ 3x2 < 24 Xi,X2>0

0 2 4 6

Рис. 5п-9. Графическое решение

8 10 12 14 X,

Графическое решение показано на рисунке 5п-9. - . ж! т ж шж5 вш ,. в Теперь давайте посмотрим, как можно использовать Таблица решения - одно Симплексный метод для получения решения. из серии решений в таблич-

Симплексная методика включает разработку о> Фор/: коерешение , i: I соответствует угловой точке

серии решении в табличной форме - таблиц решения. * области возможных реше-

Рассмотрев нижнюю строку каждой таблицы, ний. можно сразу сказать, достигнуто ли в данном случае в.шжва чгл- - лвжАвга. оптимальное решение. Каждая таблица соответствует

угловой точке области возможных решений. Первая таблица соответствует началу координат. Последующие таблицы создаются перемещением к смежной угловой точке, в направлении самой высокой нормы прибыли. Этот процесс продолжается до тех пор, пока существует положительная норма прибыли. Таким образом, процесс включает следующие шаги:

1. Составить начальную таблицу.

2. Разработать следующую таблицу, используя информацию из первой таблицы.

3. Проверить решение на оптимальность.

4. Повторять шаги 2 и 3, до тех пор пока дальнейшая оптимизация станет невозможной.

Построение начальной таблицы

Построение начальной таблицы -двухэтапный процесс. Сначала мы должны записать ограничения в виде равенств и слегка модифицировать целевую функцию. Затем мы помешаем эту информацию в таблицу и производим ряд вычислений, которые необходимы для завершения таблицы.

Перезапись целевой функции и ограничений производится с прибавлением резервных переменных, по одной для каждого ограничения. Переменные резерва представляют собой количество каждого ресурса, которое не будет использовано, если решение выполнено. В начальном решении, с каждой из реальных переменных равной нулю, решение состоит исключительно из резерва. Ограничения с добавленным резервом становятся равенствами:

(1) х,+3х2+lsi= 12

(2) 4x1+3x2+ls2= 24

При составлении таблицы полезно представить каждую резервную переменную в каждом уравнении. Следовательно, мы можем записать эти уравнения в эквивалентной форме:

(1) Х1+ЗХ2+ ls, + 0S2= 12

(2) 4x,+3x2+0s,+lS2=24

Целевая функция может быть записана в сходной форме:

Z = 4x1+5x2+ Osi+ 0s2 У переменных резерва в целевой функции нулевые коэффициенты, потому что они не вносят своего вклада в прибыль. Таким образом, подводим итоги полученной информации:

Максимизировать: Z = 4xi +5x2+ Sj + 0s2

Ограничения: (1) Х] +3x2 + IS] + 0s2 = 12 (2)4xi+3x2+Os,+ 1S2=24 Это образует основу нашей начальной таблицы, которая показана в таблице 5п-1.

Чтобы завершить исходную таблицу, нам нужны две дополнительные строки, Z и C-Z. Строка Z показывает уменьшение прибыли, которое произойдет, если одна единица переменной в этом столбце будет добавлена к решению. Строка C-Z показывает потенциал увеличения прибыли, если одна единица переменной этого столбца будет добавлена к решению.