Рассмотрим эту же задачу, представив систему в векторной форме:

Здесь векторы Р Р2, Р3, b являются двухмерными; в общем виде они представимы как (о а2)т. На рис. 7.3 на плоскости (alt а2) показаны векторы данной системы. Например, вектор b = (4, 2)т, где а, = 4, а2 = 2.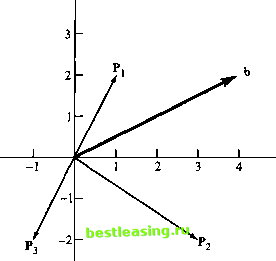

Рис. 7.3. Векторное представление системы уравнений

Поскольку у нас только два уравнения (т = 2), базис должен состоять из двух векторов, выбранных среди Р Р2 и Р3. Из рис. 7.3 видно, что пары векторов (Р Р2) и(Р2Р3) могут быть базисами, поскольку векторы в этих парах независимы. Но пара векторов (Р Р3) не может составить базис, так как эти векторы линейно зависимы.

Алгебраический подход к определению базиса требует, чтобы определитель матрицы, составленной из векторов, претендующих на роль базисных, был отличен от нуля. Вычисления определителей показывают, что пары векторов (Рр Р2) и (Р2 Р3) будут базисами, а векторы (Р Р3) не могут составить базис.

det(P Р,) = det Q j = (1 х (-2)) - (2 х 3) = -8 * 0. det(P2,P3) = detj Ъ ~М = (Зх(-2))-(-2х(-1)) = -80.

det(P1,P3) = det

fl -Г 2 -2

= (1х(-2))-(2х(-1)) = 0.

УПРАЖНЕНИЯ 7.1.2

1. Представленные ниже системы уравнений а) и б) имеют единственные базисные решения, система в) - бесконечно много решений, а г) не имеет решения. Докажите это, представив решения графически на плоскости. На основании данных примеров выведите общие закономерности, определяющие у системы уравнений единственное решение, бесконечно много решений или отсутствие решений.

а) в)

х,+3х, = 2, Зх,+х2 = 3. 2х, + 6х2 = 4, х, + 3х2 = 2.

б) г)

2*, + Зх2 = 1, 2х,-х2 = 2. 2л;, - 4х2 = 2, -х, + 2х2 = 1.

Определите графически, какая из следующих систем уравнений имеет единственное решение, бесконечно много решений или не имеет решений.

а) в) Д)

1 -з)Ц (l, -1

г) е)

<\ О

3. Дана следующая система уравнений.

Определите, какой из следующих наборов векторов образует базис.

a) (Р Р2, Р3)

b) (Р Р2, Р4)

c) (Р2,Р3,Р4)

d) (Р Р2, Р3, Р4)

4. Истинны или ложны следующие утверждения?

a) Если матрица В не вырождена, то система ВХ = b имеет единственное решение.

b) Система ВХ = b не имеет решения, если матрица В вырождена и вектор b независим относительно векторов, составляющих матрицу В.

c) Система ВХ = b имеет бесконечно много решений, если матрица В вырождена и вектор b зависим относительно векторов, составляющих матрицу В.

7.1.2. Матричное представление симплекс-таблиц

В этом разделе мы используем матричную алгебру для построения симплекс-таблиц. Рассмотрим стандартную задачу ЛП

максимизировать г = СХ при ограничениях АХ = b, X > 0.

Эту задачу ЛП можно также записать следующим образом.

Для любой симплексной итерации будем обозначать через Хв базисный вектор переменных, а через Св - вектор коэффициентов целевой функции, соответствующих этому базису. Поскольку все небазисные переменные равны нулю, стандартная задача ЛП будет сведена к задаче с целевой функцией г = СВХВ и ограничениями ВХВ = Ь, где текущее решение удовлетворяет следующему уравнению.

Здесь при обращении матрицы использовались формулы из раздела А.2.7.

Симплекс-таблица получается из исходной задачи ЛП путем вычислений по следующей формуле.

С, В

-С А

Выполнив вычисления по этой формуле, получаем такую симплекс-таблицу.

В 1 Р,

В этой таблице необходимо вычислить только обратную матрицу В-1, так как другие элементы таблицы получаются из исходных данных задачи.

Представленная симплекс-таблица имеет большое значение, так как является основой всех вычислительных алгоритмов линейного программирования. В частности, на ней основаны модифицированный симплекс-метод, метод решения задач с ограниченными переменными и метод декомпозиции, которые будут описаны в следующих разделах.

Пример 7.1.3

Рассмотрим следующую задачу ЛП.

Максимизировать г = дс, + 4х2 + 7х3 + 5х4

при ограничениях

2хх +хг + 2х3 + 4.х4 = 10, 3*, - х2 - 2х3 + 6xt = 5, х х2, х3, xt>0. Пусть В = (Р Р2) является допустимым базисом.