Последний пример показывает, что любую задачу ЛП можно с помощью преобразований привести к виду, который необходим для выполнения алгоритма Кармаркара. Но эти преобразования громоздкие и неочевидные, поэтому их редко используют на практике. Существуют различные модификации алгоритма, которые не требуют обязательного выполнения второго условия (min г = 0).

Пример 7.7.2

Рассмотрим еще раз задачу из примера 7.7.1.

Максимизировать г=у1+у2

при ограничениях

Уг + 2уг<2,

Начнем с формулировки прямой и двойственной задач.

Прямая задача Двойственная задача

Максимизировать уо = yi + Уг при ограничениях yi + 2у2 < 2,

Уь Уг 2 0.

Ограничения этих задач в стандартной форме запишутся так:

у1 + 2уг+у3 = 2,у3>0.

w,-w2 = l,w2>0. (1)

Из условия оптимума у0 = w0 вытекает, что

yi+y2-2Wl = 0. (2)

Выбираем достаточно большое число М, чтобы выполнялось неравенство

y.+y. + yw. + wM. (3)

Теперь путем введения дополнительной переменной преобразуем неравенство (3) в равенство:

У1+У2 + Уз + и>х + и>2 + 51=М, SjO. (4)

Далее введем новую переменную s2 такую, что следующие два равенства, вытекающие из равенства (4), будут выполняться тогда и только тогда, когда s2 = 1.

</i + У г + Уз + wi + w2 + si - S2M = °.

y1 + y1 + ya + wl+w2 + sl+s2 = M + 1. (5)

При условии s2 = 1, что обусловливают равенства (5), ограничения (1) можно записать как

У, + 2</2 + </,-282 = 0.

ш, - и>2 - ls2 = 0. (6)

Минимизировать щ = 2щ при ограничениях

w,>\ 1 2*,>lj

Wi > 0.

Теперь определим новые переменные xv х2, х7 на основе соотношений

у~(М + 1)хг]=1, 2,3,

(М + l)Xj, j = 4, 5,

Sl = (M+l)x6, s2 = (M + l)x7.

Подставляя последние выражения в равенства (2), (5) и (6), получим новые ограничения в виде равенств.

+ х,- 2ха = О,

, + х2 + х3 + х4 + хь + хе - Мх7 = О, [ + х2 + х3 + х4 + х5 + х6 + х7 = 1, + 2х2 + х3 - 2х7 = О, х5 -~ х7 О, .>0,;=1,2, 7.

Теперь осталось ввести искусственную переменную xs в левую часть каждого ограничения - эта переменная будет новой целевой функцией, которую следует минимизировать. Если прямая задача имеет допустимое решение, то минимум этой целевой функции будет равен нулю. Но алгоритм Кармаркара дополнительно требует, чтобы точка

х-(- 1111111

удовлетворяла системе АХ = 0. Это условие можно выполнить для однородной системы (т.е. для системы, у которой правые части уравнений равны нулю), если соответствующий коэффициент при искусственной переменной хе в любом уравнении систем будет равен сумме всех остальных коэффициентов этого уравнения. С учетом этого замечания получаем следующую преобразованную задачу ЛП.

Минимизировать z = xs

при ограничениях

jCj 4- х2 - 2х4 - 0х3 = О, х

+ 2х2 + х3 - 2х7 - 2xs =

- Мх7 - (6 - M)xg = О, х, + %гх, + х, - %гхч - zxs = О,

ОС OCrj I ) у

х, + х, + я, 4- х, + ли 4- х* 4- х, + xa = 1, x>0,j=l,2, ...,8.

Отметим, что решение этой задачи дает оптимальные решения как прямой, так и двойственной задач.

Теперь опишем основные этапы алгоритма Кармаркара. На рис. 7.7, а показано типичное трехмерное пространство решений, определяемое однородной системой ограничений АХ = 0, состоящей из одного уравнения. В данном случае пространство решений совпадает с отрезком прямой АВ, лежащим внутри симплекса IX = 1, причем точка (1/3,1/3,1/3) является допустимой внутренней точкой пространства решений. Аналогично на рис. 7.7, б показано четырехмерное пространство решений (треугольник ABC), определяемое однородной системой ограничений, также состоящей из одного уравнения. В этом случае центром симплекса является точка (1/4, 1/4, 1/4, 1/4).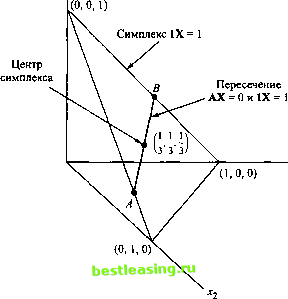

а) Трехмерное пространство решений

(о, 0, 0, 1)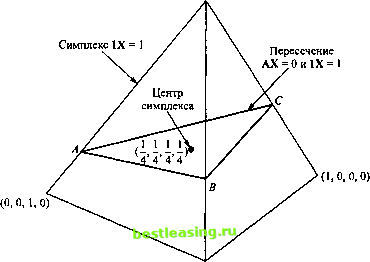

(0,1,0,0)

б) Четырехмерное пространство решений Рис. 7.7. Трех- и четырехмерный симплексы