что область 3 < jc, < 4 пространства допустимых решений задачи ЛПО не содержит целочисленных значений переменной лс, и, следовательно, может быть исключена из рассмотрения, как бесперспективная. Это эквивалентно замене исходной задачи ЛПО двумя новыми задачами линейного программирования ЛП1 и ЛП2, которые определяются следующим образом: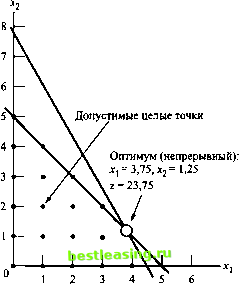

Рис. 9.5. Пространство решений задачи ЦЛП

пространство допустимых решений ЛП1 = пространство допустимых решений ЛПО

+ (х, < 3),

пространство допустимых решений ЛП2 = пространство допустимых решений ЛПО

+ (х, > 4).

На рис. 9.6 изображены пространства допустимых решений задач ЛП1 и ЛП2. Оба пространства содержат все допустимые решения исходной задачи ЦЛП. Это означает, что задачи ЛП1 и ЛП2 не потеряют решения начальной задачи ЛПО.

Если мы продолжим разумно исключать из рассмотрения области, не содержащие целочисленных решений (такие как 3 < ж, < 4), путем введения надлежащих ограничений, то в конечном счете получим задачу линейного программирования, оптимальное решение которой удовлетворяет требованиям целочисленности. Другими словами, будем решать задачу ЦЛП путем решения последовательности непрерывных задач линейного программирования.

Новые ограничения х, < 3 и i, > 4 взаимоисключаемы, так что задачи ЛП1 и ЛП2 необходимо рассматривать как независимые задачи линейного программирования, что и показано на рис. 9.7. Дихотомизация задач ЛП - основа концепции ветвления в методе ветвей и границ. В этом случае хх называется переменной ветвления.

Оптимальное решение задачи ЦЛП находится в пространстве допустимых решений либо задачи ЛП1, либо ЛП2. Следовательно, обе подзадачи должны быть решены.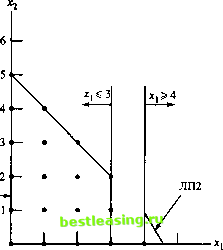

ЛП1-

0 1 2 3 4 5

Рис. 9.6. Пространства решений задач ЛП1 и ЛП2

Выбираем сначала задачу ЛП1 (выбор произволен), имеющую дополнительное ограничение х, < 3.

Максимизировать z = 5х, + 4х2

при ограничениях

х, + х2 < 5, 10х, + 6х2<45, *,<3, хр х2>0.

х1=3,75,х2= 1,25, z = 23,75

х1 = 3,х2=2, z = 23 Нижняя граница (оптимум)

х, = 4, х2= 0,83, z = 23,33

Рис. 9.7. Ветвление по переменной х; для создания задач ЛП1 и ЛП2

Оптимальным решением задачи ЛП1 (которое можно получить с помощью метода решения задач с ограниченными переменными, изложенного в разделе 7.3) являет-ся х, = 3, х2 = 2 и 2 = 23.

Оптимальное решение задачи ЛП1 удовлетворяет требованию целочисленности переменных Xj и х2. В этом случае говорят, что задача ЛП1 прозондирована. Это означает, что задача ЛП1 не должна больше зондироваться, так как она не может содержать лучшего решения задачи ЦЛП.

Мы не можем в этой ситуации оценить качество целочисленного решения, полученного из рассмотрения задачи ЛП1, ибо решение задачи ЛП2 может привести к лучшему целочисленному решению (с большим значением целевой функции г). Пока мы можем лишь сказать, что значение г = 23 является нижней границей оптимального (максимального) значения целевой функции исходной задачи ЦЛП. Это значит, что любая нерассмотренная подзадача, которая не может привести к целочисленному решению с большим значением целевой функции, должна быть исключена из рассмотрения, как бесперспективная. Если же нерассмотренная подзадача может привести к лучшему целочисленному решению, то нижняя граница должна быть надлежащим образом изменена.

При значении нижней границы z = 23 исследуем задачу ЛП2 (единственную оставшуюся нерассмотренную подзадачу). Так как в задаче ЛПО оптимальное значение целевой функции равно 23,75 и все ее коэффициенты являются целыми числами, то невозможно получить целочисленное решение задачи ЛП2 (пространство решений которой более узко, чем в задаче ЛПО), которое будет лучше существующего. В результате мы отбрасываем подзадачу ЛП2 и считаем ее прозондированной.

Реализация метода ветвей и границ завершена, так как обе подзадачи ЛП1 и ЛП2 прозондированы (рассмотрение первой привело к целочисленному решению, а второй - к заключению, что ее возможное целочисленное решение не может быть лучше существующего). Следовательно, мы заключаем, что оптимальным решением задачи ЦЛП является решение, соответствующее нижней границе, а именно х, = 3, х2 = 2 и z = 23.

Остались без ответа два вопроса, связанные с реализацией описанной вычислительной процедуры.

1. Можно ли было в задаче ЛПО выбрать переменную хг в качестве переменной ветвления вместо х,?

2. Можно ли было при выборе подзадачи для зондирования решить сначала задачу ЛП2 вместо ЛП1?

Ответы на оба вопроса положительные. Однако последующие вычисления могут значительно отличаться. Ситуация, когда первой решается задача ЛП2, иллюстрируется схемой вычислений (рис. 9.8), подтверждающей высказанную мысль. Оптимальным решением задачи ЛП2 является х, = 4, х2 = 0,83 и z = 23,33 (проверьте с помощью программы TORA).

Поскольку значение переменной х2 (= 0,83) не является целым числом, задача ЛП2 исследуется дальше. Рассматриваем подзадачи ЛПЗ и ЛП4, используя ветви х2<0 и х2 > 0 соответственно. Это означает, что

пространство решений ЛПЗ = пространство решений ЛП2 + (х2 < 0) = = пространство решений ЛПО + (х, > 4) +(х2 < 0),

пространство решений ЛП4 = пространство решений ЛП2 + (х2 > 1) = = пространство решений ЛПО + (х, > 4) +(х2 > 1).