Используя программу TORA в автоматическом режиме, ответьте на следующие вопросы.

a) Сколько подзадач было решено прежде, чем было найдено оптимальное решение?

b) Сколько подзадач было решено прежде, чем была проверена оптимальность найденного решения?

2. Дана следующая задача ЦЛП.

Максимизировать z - 18х, + 14х2 + 8х3 при выполнении условий

15х, + 12х2+ 7х3 < 43,

х1( х2, х3 - неотрицательные целые.

В системе TORA в режиме пошагового выполнения создайте дерево подзадач с вычислением границ целевой функции и без такового. Как повлияет знание границ целевой функции на количество сгенерированных подзадач? Для сравнения всегда выбирайте переменную ветвления с наименьшим индексом и зондируйте все задачи в текущей строке слева направо, затем переходите на следующую строку.

3. Вернитесь к задаче из упражнения 2. Преобразуйте эту задачу в задачу ЦЛП с двоичными переменными, затем решите ее в программе TORA в автоматическом режиме. Сравните размеры деревьев подзадач в каждом из упражнений.

4. В следующей задаче ЦЛП с двоичными переменными с помощью TORA сгенерируйте дерево подзадач.

Максимизировать z = Зх, + 2х2 - 5х3 - 2х4 + Зхь

при выполнении условий

х, + х2 + х3 + 2х4 + х6 < 4, 7х, + Зх3 - 4х4 + Зх5 < 8, ИхбХг + Зх.-ЗхЗ, хр х2, х3, х4, х5 = О или 1.

5. Используя программу TORA в режиме пошагового выполнения, покажите, что следующая задача не имеет допустимого решения.

Максимизировать z = 2х, + х2

при выполнении условий

10х, + 10х2 < 9, Юх, + 5х2> 1, х х2 = 0 или 1.

6. С помощью TORA создайте дерево подзадач в методе ветвей и границ для следующей частично-целочисленной задачи и найдите ее оптимальное решение.

Максимизировать z = х, + 2х2 - Зх3

при выполнении условий

Зх, + 4х2 - х3 < 10, 2х, - Зх2 + 4х3 < 20, х х2 неотрицательные целые, х3>0.

7. В системе TORA создайте дерево подзадач для следующей задачи, полагая, что выполняется только одно ограничение.

Максимизировать г = хх + 2х2 - Зх3

при выполнении условий

20х1 + 15л:.!-л:з<10, 12x1 + 3x2 + 4x3<13, х х2, х3>0.

8. Преобразуйте представленную ниже задачу в частично-целочисленную, после чего в системе TORA сгенерируйте для нее дерево подзадач. Каким будет оптимальное решение?

Максимизировать z = хх + 2х2 + 5х3

при выполнении условий

j-jc1 + 10jc2 - 3xs > 15, 2х1+х2 + х3<10, xv х2, х3 > 0.

9.2.3. Метод отсекающих плоскостей

Данный метод, как и метод ветвей и границ, начинает работу с оптимального решения обычной (непрерывной) задачи линейного программирования. Однако вместо ветвления и построения границ этот метод видоизменяет пространство допустимых решений, последовательно прибавляя специальным образом построенные ограничения (именуемые отсечениями). Рассмотрим сначала идею этого метода на графическом примере, а затем покажем, как отсечения строятся алгебраически.

Пример 9.2.2

Продемонстрируем применение метода отсекающих плоскостей для решения следующей задачи ЦЛП.

Максимизировать z = 7х, + 10х2

при ограничениях

-хх +3х2<6, 7х1+х3<35, х х2> 0 и целые.

Данный метод путем добавления отсечений (отсекающих плоскостей) преобразует пространство допустимых решений соответствующей задачи линейного программирования в выпуклый многогранник, вершина которого, соответствующая оптимуму, является целочисленной и представляет решение исходной задачи. На рис. 9.12 показан пример двух таких отсечений. Мы начинаем с оптимального решения непрерывной задачи линейного программирования (хх, х2) = (4,5, 3,5) и z = 66,5. Затем прибавляем отсечение I, которое вместе с ограничениями исходной задачи линейного программирования приводит к оптимальному решению (х х2) = (4 у , 3) с z = 62. После этого прибавляется отсечение II, которое вместе с отсечением I и исходными ограничениями приводит к оптимальному решению (xv х2) - (4, 3) с z = 58. Последнее решение является полностью целочисленным, как и требуется.

Прибавленные отсечения не отбрасывают ни одной исходной допустимой целочисленной точки, но должны проходить по меньшей мере через одну целочисленную точку (допустимую или недопустимую). Этим основным требованиям должно удовлетворять любое отсечение.

В общем случае может потребоваться любое (конечное) число отсечений для достижения полностью целочисленной экстремальной точки. В действительности количество необходимых для этого отсечений не зависит от размерности задачи в том смысле, что для решения задачи с небольшим количеством переменных и ограничений может потребоваться больше отсечений, чем для задачи большой размерности.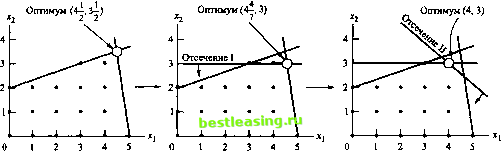

Рис. 9.12. Последовательность построения отсечений

Метод отсекающих плоскостей начинает работу с решения непрерывной задачи линейного программирования. В симплекс-таблице, соответствующей оптимальному решению задачи линейного программирования, следует выбрать одну из строк (называемую производящей), для которой базисная переменная нецелочисленная. Искомое отсечение строится на основании дробных составляющих коэффициентов производящей строки. По этой причине его называют дробным отсечением. Покажем построение дробного отсечения на нашем примере.

При дополнительных переменных хъ и х4 для ограничений 1 и 2 оптимальная симплекс-таблица исходной задачи имеет следующий вид.

Оптимальным непрерывным решением является х1 = 4,5, х2 = 3,5, хг = 0, xt = О иг = 66,5. Целочисленное отсечение получается в предположении, что все переменные задачи являются целочисленными. Поскольку коэффициенты исходной целевой функции являются целочисленными, то и значение г, соответствующее целочисленному решению, должно быть целочисленным.

Информация, содержащаяся в симплекс-таблице, соответствующей оптимальному решению, может быть записана в виде следующих уравнений.

z-уравнение: z + x3+±х4 = 66,

х2-уравнение: хг+хг +*4 =3-

Xj-уравнение: х, -Jx, + х4 =4.