Есть две возможности исправить эту ситуацию.

1. Можно умножить все ограничения на соответствующую константу для устранения дробей. Например, приведенное выше ограничение умножается на 6, что приводит к неравенству 6л:1 + 2х2 < 39. Любое целочисленное решение переменных х, и х2 автоматически дает целочисленное значение дополнительной переменной. Однако этот тип преобразования применим лишь для простых ограничений, так как значения необходимых целочисленных коэффициентов в некоторых случаях могут быть чрезвычайно большими.

2. Можно использовать специальные отсечения, именуемые частично-целочисленными. Они ориентированы на решение задач, в которых лишь часть переменных должна принимать целочисленные значения, а остальные (включая дополнительные) остаются непрерывными. Детальное изложение таких отсечений в этой главе не рассматривается (см. [3]).

УПРАЖНЕНИЯ 9.2.3

1. В примере 9.2.2 покажите графически, может ли каждое из следующих ограничений служить в качестве правильного отсечения.

a) xt + 2х2 < 10.

b) 2х, + х2<10.

c) Зх2<10.

d) Зх1+х2<15.

2. В примере 9.2.2 покажите графически, как следующие два правильных отсечения могут привести к оптимальному целочисленному решению.

Отсечение I. х, + 2х2 < 10.

Отсечение II. Зхх + х2 < 15.

3. Запишите отсечения I и II в примере 9.2.2 через уравнения для переменных х, и х2 и покажите, что они совпадают с отсечениями, которые графически показаны на рис. 9.12.

4. Покажите, что дробное отсечение не приводит к допустимому решению в приведенной ниже задаче, если не устранены все дроби в ограничении.

Максимизировать z = хх + 2х2

при ограничениях

1 13

X. + -Х, <-,

1 2 - 4 х х2 > 0 и целые.

5. Решите следующие задачи методом отсекающих плоскостей и сравните оптимальное целочисленное решение с решением, полученным путем округления соответствующего оптимального непрерывного решения.

а) Максимизировать г = 4х, + 6х2 + 2хъ

при ограничениях

4х, - 4х2 < 5,

-х, + 6х2< 5,

-х, + х2 + х3< 5,

х х2, х3> 0 и целые.

Ь) Максимизировать г = Зх, 4- хг + Зх3 при ограничениях

-хл +2х2 + х3<4, 4х2 - Зх3 < 2, х1-3х2 + 2х3<3, xv х2, х3 > 0 и целые.

9.2.4. Вычислительный взгляд на задачи ЦЛП

На сегодняшний день, несмотря на 40 лет интенсивных исследований, не существует вычислительного алгоритма, приемлемого для решения всех разнообразных задач целочисленного программирования. Из представленных в этой главе двух алгоритмов метод ветвей и границ считается более эффективным - практически все коммерческие программы, предназначенные для решения задач ЦЛП, используют этот метод. Метод отсекающих плоскостей более сложен и менее надежен, кроме того его реализация порождает серьезные проблемы, связанные с ошибками машинного округления. Было много попыток сделать этот метод эффективным для компьютерных вычислений, но они не увенчались большими успехами. В большинстве случаев метод отсекающих плоскостей используется как дополнительный метод при решении подзадач, генерируемых в процессе применения метода ветвей и границ.

Наиболее важным фактором, влияющим на процесс вычислений в целочисленном программировании, является количество целочисленных переменных. Существующие алгоритмы не решают задачу ЦЛП последовательно, т.е. не позволяют получать промежуточные целочисленные решения, отличные от оптимального, поэтому с вычислительной точки зрения в задаче ЦЛП необходимо ограничиться по возможности меньшим числом переменных, принимающих целочисленные значения. Следующие советы могут оказаться полезными при решении практических задач.

1. Аппроксимировать целочисленные переменные непрерывными, где это возможно.

2. Сузить, насколько возможно, интервалы допустимых значений целочисленных переменных.

3. Избегать в модели ЦЛП использования нелинейных функций.

Уровень развития методов решения целочисленных задач не удовлетворяет требованиям, которые диктуются их практической важностью. Маловероятно, что в целочисленном программировании будет получен новый теоретический прорыв. Представляется более вероятным, что новые технологические достижения в области компьютерной техники могут предложить новые пути повышения эффективности алгоритмов решения задач ЦЛП.

9.3. ЗАДАЧА КОММИВОЯЖЕРА

Задачи такого типа известны под общим названием задача коммивояжера, в классической формулировке которой коммивояжер пытается определить кратчайший маршрут для одноразового посещения п городов. По существу, эта задача является задачей о назначениях с дополнительными ограничениями, которые гарантируют исключение из оптимального решения неполных замкнутых маршрутов. (В задаче коммивояжера замкнутый маршрут, проходящий через

каждый пункт только один раз, называется циклом; цикл, проходящий через все пункты, называется полным, в противном случае - частичным или подциклом.) В задаче коммивояжера с п городами можно определить такие переменные:

1,если город j достижим из города i, У [0, в противном случае.

Имея значения dtj, расстояния от города i до города j (считается, что йц = °° при i=j), задачу коммивояжера можно формализовать следующим образом.

Минимизировать г = ХХЛ

при ограничениях

£х = 1,1=1,2, п<

7=1 и

хц = 0 или 1,

решение должно быть полным циклом.

Ограничения задачи, кроме последнего, определяют обычную задачу о назначениях (см. раздел 5.4). В общем случае нет гарантии, что оптимальное решение задачи коммивояжера может быть получено путем решения соответствующей задачи о назначениях, т.е., что оптимальное решение задачи о назначениях образует полный цикл. Более вероятно, что оно будет содержать частичные циклы, соединяющие вместе некоторые подмножества узлов сети. На рис. 9.13 показана задача коммивояжера, состоящая из 5-ти городов. Ребра, соединяющие узлы (города) сети, соответствуют дорогам с двухсторонним движением. На этом рисунке показано решение задачи коммивояжера и частичные циклы, соответствующие решению задачи о назначениях. Если задача о назначениях формирует полный цикл, то это будет оптимальным решением задачи коммивояжера. Если оптимальное решение задачи о назначениях состоит из нескольких частичных циклов, то в эту задачу добавляются специальные ограничения, удаляющие решения с частичными циклами. Такие ограничения будут показаны далее в этом разделе.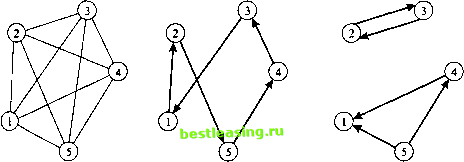

Задача S-ти городов Решение задачи коммивояжера Решение задачи о назначениях (х12 - Хи - xw - х43 - х31 - 1) (хи - хп - х13 - хн - х41 - 1)

Рис. 9.13. Пример задачи коммивояжера для 5-ти городов