Старт м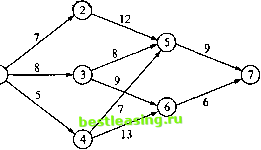

Рис. 10.1. Сеть дорог для примера 10.1.1

Мы можем решить эту задачу посредством полного перебора всех маршрутов между узлами 1 и 7 (имеется пять таких маршрутов). Однако в большой сети полный перебор является неэффективным с вычислительной точки зрения.

Чтобы решить эту задачу с помощью методов динамического программирования, сначала разделим ее на этапы. Вертикальные пунктирные линии на рис. 10.2 очерчивают три этапа задачи. Далее выполняются вычисления для каждого этапа в отдельности.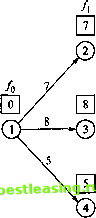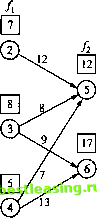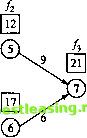

Рис. 10.2. Декомпозиция задачи на три этапа

Общая задача состоит в вычислении кратчайших (постепенно накапливаемых) расстояний ко всем вершинам этапа с последующим использованием этих расстояний в качестве исходных данных для следующего этапа. Рассматривая узлы, относящиеся к первому этапу, замечаем, что каждый из узлов 2, 3 и 4 связан с начальным узлом 1 единственной дугой (рис. 10.2). Следовательно, для первого этапа имеем следующее.

Этап 1. Итоговые результаты.

Кратчайший путь к узлу 2 равен 7 миль (из узла 1).

Кратчайший путь к узлу 3 равен 8 миль (из узла 1).

Кратчайший путь к узлу 4 равен 5 миль (из узла 1).

Далее переходим ко второму этапу для вычисления кратчайших (накопленных) расстояний к узлам 5 и 6. Рассматривая узел 5 первым, из рис. 10.2 замечаем, что

10.1. Рекуррентная природа вычислений ДП

есть три возможных маршрута, по которым можно достичь узла 5, а именно (2, 5), (3, 5) и (4, 5). Эта информация вместе с кратчайшими расстояниями к узлам 2, 3, и 4 определяет кратчайшее (накопленное) расстояние к узлу 5 следующим образом.

Кратчайший

I = min

чпуть к узлу 5 I =2.з.4

Кратчайший (Расстояние от путь к узлу i J узла / к узлу 5, 7 + 12 = 19

8+ 8 = 16 5+ 7 = 12

Аналогично для узла 6 имеем следующее.

Кратчайший \( Кратчайший

= тЫ

путь к узлу 6) =3 4 И путь к узлу i

-12 (изузла4).

Расстояние от чузла ( к узлу 6

S+ 9 = 17 тт< ? = 17 (изузла3).

15+ 13 = 18 1

Этап 2. Итоговые результаты.

Кратчайший путь к узлу 5 равен 12 миль (из узла 4).

Кратчайший путь к узлу 6 равен 17 миль (из узла 3).

Последним шагом является третий этап. Конечный узел 7 можно достичь как из узла 5, так и 6. Используя итоговые результаты этапа 2 и расстояния от узлов 5 и 6 к узлу 7, получаем следующее.

Кратчайший4 путь к узлу 1 /

12 + 9 = 21 тт{ } = 21 (из узла 5).

17 + 6 = 23 v У

Этап 3. Итоговые результаты.

Кратчайший путь к узлу 7 равен 21 миле (из узла 5).

Приведенные вычисления показывают, что кратчайшее расстояние между узлами 1 и 7 равно 21 миле. Города, через которые проходит кратчайший маршрут, определяются следующим образом. Из итоговых результатов третьего этапа следует, что узел 7 связывается с узлом 5. Далее из итоговых результатов второго этапа следует, что узел 4 связывается с узлом 5. Наконец, из итоговых результатов первого этапа следует, что узел 4 связывается с узлом 1. Следовательно, оптимальным маршрутом является последовательность 1-> 4-* 5-* 7.

Теперь покажем, как рекуррентные вычисления динамического программирования можно выразить математически. Пусть Дх,-) - кратчайшее расстояние до узла х, на этапе /, d(xLljci) - расстояние от узла до узла дг,. Тогда / вычисляется на основе значений fLl с помощью следующего рекуррентного уравнения.

/(*,)= min {rf(*w,x,) + /,-i(*,-,)}. 1 = 1.2,3.

все допустимые L 1

I*.-! -x, )-маршругы

При / = 1 полагаем /0(*0) = 0. Это уравнение показывает, что кратчайшие расстояния f{x) на этапе i должны быть выражены как функции следующего узла дг,. В терминологии динамического программирования дг, именуется состоянием системы на этапе /.

В действительности состояние системы на этапе i- это информация, связывающая этапы между собой, при этом оптимальные решения для оставшихся этапов могут приниматься без повторной проверки того, как были получены решения на предыдущих этапах. Такое определение состояния системы позволяет рассматривать каждый этап отдельно и гарантирует, что решение является допустимым на каждом этапе.

Определение состояния системы приводит к следующему унифицированному положению.

Принцип оптимальности. На каждом этапе оптимальная стратегия определяется независимо от стратегий, использованных на предыдущих этапах.

Применение принципа оптимальности демонстрируется вычислениями из примера 10.1.1. Например, на этапе 3 мы используем кратчайшие пути к узлам 5 и 6 и не интересуемся, как эти узлы были достигнуты из узла 1.

УПРАЖНЕНИЯ 10.1

1. Решите задачу из примера 10.1.1, предполагая, что используются следующие длины маршрутов:

d(l, 2) = 5,(1,3) = 9,(1,4) = 8,

d(2, 5) = 10, rf(2, 6)= 17,

d(3, 5) = 4, d(3, 6)= 10,

d(4, 5) = 9, d(4, 6) = 9,

d(5, 7) = 8,

d(6,1) = 9.

2. Я - заядлый турист. Прошлым летом мы с другом отправились в пятидневный поход по прекрасным Белым Горам в штате Нью-Гемпшир. Мы решили ограничить наше путешествие территорией, на которой расположены три хорошо известные вершины: Вашингтон, Джефферсон и Адаме. Гора Вашингтон имеет шестимильную тропу от подножия до вершины. Аналогичные тропы гор Джефферсона и Адамса имеют длину 4 и 5 миль соответственно. Тропы, соединяющие подножия этих трех гор, имеют следующую длину: 3 мили между вершинами Вашингтона и Джефферсона, 2 мили между вершинами Джефферсона и Адамса и 5 миль между вершинами Адамса и Вашингтона. В первый день мы стартовали от подножия вершины Вашингтона и вернулись в эту же точку к концу пятого дня. Нашей целью было пройти как можно более длинный путь. Мы также решили подниматься каждый день только на одну вершину и располагаться лагерем у подножия той горы, на которую мы решили восходить на следующий день. Кроме того, мы решили, что не будем подниматься на одну и ту же вершину в течение двух дней подряд. Каким было расписание нашего похода?

10.2. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ ПРЯМОЙ И ОБРАТНОЙ ПРОГОНКИ

В примере 10.1.1 вычисления проводились последовательно: от первого этапа до третьего. Такая последовательность вычислений известна как алгоритм прямой прогонки. Этот же пример может быть решен с помощью алгоритма обратной прогонки, в соответствии с которым вычисления проводятся от третьего этапа до первого.