cov{x x,} = М{(*, -М{xt})(x2 -М{х2})} = М\х{х2 -х,М[х2}~х2М{х,} + М{хх}М{х2}} = = М{х,х2}-М{х,}М{х2}.

Если хх и х2- независимые случайные величины, то М{хххг) = М{хх)М{х2) hcov{x хг) = 0. Обратное утверждение неверно в том смысле, что две зависимые случайные величины могут иметь ковариацию, равную нулю.

Пример 12.3.3

Партия изделий содержит четыре дефектных (Д) и шесть качественных (К) изделий. Случайным образом выбирается и проверяется одно изделие. Затем, не возвращая его, выбирают и тестируют другое. Пусть случайные величины хх и х2 представляют исходы тестирования первого и второго изделий соответственно.

1. Определим плотность совместного распределения вероятностей случайных величин х, и х2.

2. Найдем маргинальную плотность вероятности случайной величины х2.

3. Предположим, мы получаем 5 долл. за каждое качественное изделие из выбранных и платим 6 долл., если изделие бракованное. Найдем математическое ожидание и дисперсию выигрыша после двух испытаний.

Обозначим через р(хх, х2) плотность совместного распределения вероятностей случайных величин х, и х2, а через рДх,) и р2(х2) - их маргинальные плотности вероятностей. Определим сначалар,(х,) как

Мы знаем, что исход х2 второго испытания зависит от xv По этой причине для определения р2(х2) сначала определим плотность р(хх, х2) совместного распределения вероятностей случайных величин хг и х2, после чего можно будет определить маргинальную плотность вероятности р2(х2). Имеем

Для определения р(х1У х2) воспользуемся формулой Р{АВ} = Р{А В}Р{В} (см. раздел 12.1.2). Получаем следующее.

Pi(K) = - = 0,

6 А(Д) = = 0,4.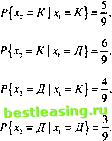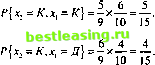

Представим теперь плотность совместного распределения следующим образом.

Маргинальные плотности распределения вероятностей p,(#i) и р2(х2) могут быть определены посредством суммирования элементов (соответственно) столбцов или строк в таблице, представляющей значения плотности совместного распределения. Интересно отметить, что, вопреки интуиции, здесь рДдс,) = рг(х2).

Математическое ожидание выигрыша можно определить из совместного распределения, если принять, что изделие К дает 5 долл., а изделие Д - 6. Следовательно,

ожидаемый выигрыш = (5 + $)Jj + {$~{jj +

+ ( + 5)(±) + Н-6)(2) = 1,20.

Тот же результат можем получить, принимая во внимание, что математическое ожидание выигрыша после двух испытаний равно сумме математических ожиданий после каждого испытания в отдельности.

ожидаемый выигрыш =(ожидаемый выигрыш после 1-го испытания)+

+(ожидаемый выигрыш после 2-го испытаиия)=

= 0,60 + 0,60 = 1,20.

Для вычисления дисперсии общего выигрыша заметим, что

1){выигрыша} = £){1-го выигрыша} + £){2-го выигрыша} +

+ 2cov{l-ro выигрыша, 2-го выигрыша}.

Так как р,(х,) = р2(х2), то D{l-ro выигрыша} = D{2-ro выигрыша}. Для вычисления дисперсии воспользуемся формулой

D{x)=M{x2}-(M{x})\

Следовательно,

£){1-го выигрыша} =

-0, б2 =29,04.

Далее для вычисления ковариации применим формулу

cov{x1,x2} = М {хх2} - М {х М {хг}.

При вычислении значения М{х1х2) нужно знать плотность совместного распределения вероятностей случайных величин хх и х2. Имеем

ковариация:

-0,6x0,6 = -3,23.

Итак,

дисперсия = 29,04 + 29,04 + 2(-3,23) = 51,62.

УПРАЖНЕНИЕ 12.3.3

1. Плотность совместного распределения вероятностей p(xv хг) случайных величин ас, и х2 имеет следующий вид.

a) Найдите маргинальные плотности вероятностейрДх,) ир2(х2).

b) Являются ли случайные величины и х2 независимыми?

c) Вычислите М{хх + х2).

d) Найдите cov{x хг).

e) Вычислите D{5x, - 6х2}.

12.4. НЕКОТОРЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ

В разделах 12.2 и 12.3 мы рассмотрели равномерные распределения (дискретные и непрерывные). В этом разделе рассматриваются еще четыре распределения случайных величин, которые часто используются в теории исследования операций, - дискретные (биномиальное и Пуассона) и непрерывные (экспоненциальное и нормальное).

12.4.1. Биномиальное распределение

Предположим, предприниматель изготавливает некоторые изделия партиями по п единиц в каждой. Предыдущий опыт свидетельствует, что вероятность появления бракованного изделия в каждой партии равна р. Необходимо определить плотность вероятности числа бракованных изделий в партии.

тт X Х\(П~Х)\

Имеется С* = 4 -- различных возможностей получить х бракованных изделий в партии из п изделий; вероятность реализации каждой такой комбинации равна р (1 -р) ~ . Отсюда следует, что вероятность того, что в партии из п изделий имеется k бракованных, равна (что следует из закона сложения вероятностей)

Р{х = к} = Ск рк(1-р) -\ к =1,2,..., п.