

 |
 |

|
Промышленный лизинг
Методички
(a + bx°) ±t. a/2.n-2 n~2 V Мы заинтересованы в установлении для прогнозируемых значений зависимой переменной у соответствующих им интервалов предсказания (это важнее, чем доверительный интервал для среднего значения оценки). Как и следовало ожидать, интервал предсказания для значения прогнозируемой величины является более широким, чем доверительный интервал для среднего значения оценки. Действительно формула для интервала предсказания такая же, как и для доверительного интервала, но с той лишь разницей, что член 1/п под вторым квадратным корнем заменен на (п + 1)/п. Чтобы проверить, насколько линейная модель у*=а + Ьх соответствует исходным данным, необходимо вычислить коэффициент корреляции г согласно формуле: где -1<г< 1. Если г = ±1, тогда линейная модель идеально подходит для описания зависимости между у и х. В общем случае, чем ближе \г\ к 1, тем лучше подходит линейная модель. Если же г - 0, величины у и х могут быть независимыми. В действительности равенство г = 0 является лишь необходимым, но не достаточным условием независимости, так как возможен случай, когда для двух зависимых величин коэффициент корреляции будет равен нулю. Пример 13.3.1 Применим модель линейной регрессии к данным из примера 13.1.1, которые для удобства приведены в табл. 13.6. Таблица 13.6
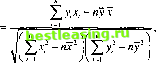 Из данных этой таблицы получаем следующее. £ уiXi = 17842, £ х, = 300, £ х; = 4900, £ у, = 1374, £ / = 80254. 1-1 ;=1 /=! i=i i=i Следовательно, 1 = 12,5, 7 = 57,25, , 17842-24x57,25x12,5 Ь =-г-= 0,58, 4900 - 24х12,52 а = 57,25-0,58х12,5 = 50. Таким образом, оценка спроса представляется формулой / = 50 + 0,58*. Например, прих = 25 получаем / = 50 + 0,58 х 25 = 64,5 единицы. Вычисляем коэффициент корреляции: 17842-24x57,25x12,5 (4900 - 24 х 12,5г) (80254 - 24 х 57,251) = 0,493. Относительно малое значение коэффициента корреляции г указывает на то, что линейная модель /= 50 + 0,58х является не совсем подходящей для исходных данных. Считается, как правило, что линейная модель подходит для исходных данных, если 0,75 < r < 1. Предположим, необходимо вычислить 95% -ный доверительный интервал для полученной линейной оценки. Для этого надо сначала вычислить сумму квадратов отклонений от аппроксимирующей прямой. В табл. 13.7 приведены результаты этих вычислений. Из табл.2 приложения В имеем f0025.22 = 2,074. Следовательно, искомый доверительный интервал имеет вид (50 + 0,58л;0) ±2,074 1205,64 1 + (/-12,5) 24-2 \ 24 4900 - 24х12,52 Это выражение можно упростить, в результате получим следующее. / (х0 -12,5) (50+ 0,58л-°)± 15,35 W0,042 + -v 1150 Чтобы продемонстрировать применение этой формулы, вычислим интервал предсказания для оценки спроса на следующий месяц (х° = 25). В этом случае коэффициент 0,042 должен быть заменен на 1,042,2 и соответствующий интервал предсказания определяется как (64,5 ±16,66) или (47,84,81,16). Следовательно, можно сказать, что с вероятностью 95 % спрос для х = 2Ъ будет находиться между 47,84 и 81,16 единицами. 2 Напомним, что определение интервала предсказания основано на формуле, определяющей доверительный интервал, где под корнем слагаемое 1/п заменено на (п + 1)/п. - Прим.ред. Таблица 13.7
£(у, -у,*) =1205,64 Вычисления регрессионного анализа обычно весьма сложны и громоздки. К счастью, нет необходимости выполнять их вручную. Excel предлагает для этого несколько средств. На рис. 13.3 показан рабочий лист с исходными данными и диалоговое окно средства Регрессия, которое предназначено для выполнения вычислений регрессионного анализа. Excel автоматически сгенерирует выходной отчет этого средства, содержащий всю необходимую информацию. Чтобы воспользоваться средством Регрессия, выберите команду Сервис=>Анализ данныхРегрессия. УПРАЖНЕНИЯ 13.3 1. Примените метод линейной регрессии к данным из упражнения 13.1.2. 2. Примените метод линейной регрессии к данным из упражнения 13.1.3. 3. Примените метод линейной регрессии к данным из упражнения 13.1.4. 4. Примените метод линейной регрессии к данным из упражнения 13.1.5. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 [ 175 ] 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 |