На рис. 16.6 S = у и величина s (< S) определяются из уравнения

M{C(s)} = M{C(S)\=K + M{C(S)}, s<S.

(Отметим, что это уравнение имеет и другое решение st > S, которое не рассматривается.)

Задача формулируется следующим образом. Какое количество продукции необходимо заказывать, если наличный запас перед размещением заказа составляет х единиц? Ответ на этот вопрос рассматривается по отдельности при выполнении следующих условий.

1. x<s.

2. s<x<S.

3. x>S.

Ситуация 1 (х < s). Так как в наличии имеется х единиц продукции, соответствующие издержки содержания запаса составляют М{С(х)}. Если заказывается любое дополнительное количество продукции у - х (у > х), то соответствующие затраты при заданной величине у равны величине М{С(у)}, которая учитывает стоимость К размещения заказа. Из рис. 16.6 следует, что

min М {С(у)} = М {C(S)} < М {С(х)}.

Следовательно, оптимальной стратегией управления запасами в этом случае будет заказ bS - х единиц.

Ситуация 2 (s < х < S). Из рис. 16.6 видно, что

M{C(x)}<mmM{C(y)) = M{C(S)}.

Следовательно, в данном случае дополнительных затрат не возникает, если новый заказ не размещается. Поэтому у = х.

Ситуация 3 (х > S). Из рис. 16.6 видно, что при у > х

М{С(х)}<М{С(у)\.

Это неравенство показывает, что в данном случае экономнее будет не размещать заказ, т.е. у = х.

Описанная стратегия управления запасами, часто именуемая (з-5)-стратегией, определяется следующим правилом.

Если х < s, делать заказ объемом S - х,

если х > s, заказывать не следует.

Оптимальность (я-5)-стратегии следует из того, что соответствующая функция затрат является выпуклой. Если это свойство не выполняется, данная стратегия перестает быть оптимальной.

Пример 16.2.2

Дневной спрос на продукцию в течение одного периода удовлетворяется мгновенно в начале периода. Спрос является случайной величиной, равномерно распределенной от 0 до 10 единиц. Стоимость хранения единицы продукции на протяжении периода равна 0,50 долл., а штраф за дефицит единицы продук-

ции- 4,50 долл. Стоимость единицы продукции равна 0,50 долл., стоимость размещения заказа - 25 долл. Необходимо определить оптимальную стратегию заказа продукции.

Определим сначала у . Имеем

р-с 4,5-0,5

= 0.8.

Так как

р + п 4,5 + 0,5

p{D<y}= \±-dD = ±

1 ho if

то 5 = у =8.

Ожидаемое значение функции затрат определяется следующим образом. M{C(y)} = 0.5(y-x) + 0.5j-l(y-D)rfD + 4,51}(D-y)rfD =

= 0,25у:-4у + 22,5-0.5*. Величина s определяется из уравнения

M{C(s)} = K + M{C(S)}.

Отсюда получаем

0,25s2 - 4s + 22,5 - 0,5* = 25 + 0,2552 - 45 + 22,5 - 0,5*. При 5 = 8 это уравнение сводится к виду

У-165 - 36 = 0.

Решением данного уравнения является s = -2 и 5=18. Значение 5 = 18 (превышающее 5) следует отбросить. Так как оставшееся значение является отрицательным (= -2), то 5 не имеет допустимого значения. Следовательно, оптимальной стратегией является отказ от размещения заказа (рис. 16.7). Такая ситуация обычно возникает тогда, когда функция затрат является плоской или когда затраты на размещение заказа превышают другие затраты модели.

М{С(е)}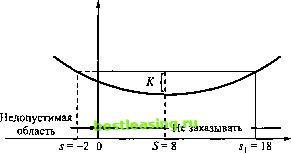

Рис. 16.7. Оптимальная стратегия размещения заказа для примера 16.2.2

УПРАЖНЕНИЯ 16.2.2

1. Определите оптимальную стратегию управления запасами для ситуации, описанной в примере 16.2.2, если предположить, что стоимость размещения заказа составляет 5 долл.

2. Пусть в одноэтапной модели, рассмотренной в разделе 16.2.1, необходимо максимизировать прибыль, при этом следует учитывать стоимость размещения заказа К. Постройте формулу для ожидаемого значения прибыли и определите оптимальный объем заказа, используя при этом информацию из раздела 16.2.1 и предполагая, что стоимость продажи единицы продукции равна г. Решите задачу при следующих данных (все величины в долл.): г= 3, с = 2, р = 4, h = 1 w. К = 10. Плотность вероятности спроса является постоянной на интервале [0, 10].

3. Решите упражнение 16.2.1.5, предполагая, что доставка орехов связана с постоянными затратами в 10 долл.

16.3. МНОГОЭТАПНЫЕ МОДЕЛИ

В этом разделе рассматривается многоэтапная модель без учета стоимости размещения заказа. Кроме того, в модели предусматривается возможность задолженности и нулевое время поставки. Предполагается также, что спрос D в каждый период описывается стационарной (независящей от времени) плотностью вероятности /(£>).

В многоэтапной модели учитывается приведенная стоимость денег. Если or(< 1) - коэффициент дисконтирования (процент скидки) для одного этапа, то сумма А спустя п этапов будет эквивалентна сумме dA в настоящий момент.

Предположим, что планирование охватывает п этапов, и неудовлетворенный спрос может оставаться таковым лишь на протяжении одного этапа. Пусть Ft(xt) - максимальная суммарная ожидаемая прибыль для этапов от i до п, определенная при условии, что xt - уровень имеющегося запаса перед размещением заказа на t-м этапе.

Используя обозначения из раздела 16.2 и предполагая, что г- удельный доход от реализации единицы продукции, сформулируем задачу управления запасами в виде следующей задачи динамического программирования (см. главу 15).

F,(лс,) = тах{-с(у, -x,)+§ rD-h{yi-D)]f{D)dD +

0

+ )[ryi+ar(D-yi)-p{D~yi)]f(D)clD +

+ a\FM{yi-D)f{D)dD), i = 1.2.....л,

где F +/(j/ - D) = 0. Величина xt может принимать отрицательные значения, так как неудовлетворенный спрос может накапливаться. Величина ar(D - у) включена во второй интеграл, поскольку D- yt представляет собой неудовлетворенный спрос на t-м этапе, который должен быть удовлетворен на этапе i + 1.

Задачу можно решить рекуррентно методами динамического программирования. Если число этапов является бесконечным, приведенное выше рекуррентное уравнение сводится к следующему.