Замкнутое множество состояний и поглощающие состояния. Множество С состояний цепи Маркова называется замкнутым, если система, однажды оказавшаяся в одном из состояний этого множества, будет находиться в множестве С в течение бесконечного интервала времени. Частным случаем замкнутого множества является единственное состояние £у с переходной вероятностью рм= \ В этом

случае состояние Ej называется поглощающим. Все состояния неприводимой цепи должны образовывать замкнутое множество, и ни одно подмножество этого множества не может быть замкнутым. Замкнутое множество С удовлетворяет всем условиям, характеризующим марковскую цепь, и, следовательно, его можно подвергнуть независимому анализу.

Пример 19.5.2

Рассмотрим цепь Маркова со следующей матрицей переходных вероятностей

Эта цепь графически представлена на рис. 19.1. Как видно из рисунка, четыре состояния не составляют неприводимую цепь, поскольку состояний 0, 1 и 2 нельзя достичь из состояния 3. Состояние 3 образует замкнутое множество и, таким образом, является поглощающим. Можно также утверждать, что состояние 3 соответствует неприводимой цепи Маркова.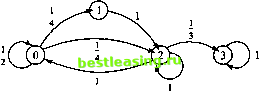

Рис. 19.1. Различные виды состояний цепи Маркова

Первое время возвращения. Важным понятием в теории марковских цепей является первое время возвращения. Система, первоначально находящаяся в состоянии Ejt может вернуться в первый раз в это же состояние через п шагов, п > 1. Число шагов, за которое система возвращается в состояние Ejt называется первым временем возвращения.

Обозначим через вероятность того, что первое возвращение в состояние Ej

состоится на л-м шагу. Тогда при заданной матрице переходных вероятностей

Р = piy /j можно определить следующим образом:

Г В J JJ J JJ rjj!

/(.2, = Р(2)-/(У.

J JJ JJ J л г II

По индукции нетрудно показать, что

/< > = < > у /.-) (.-).

,0 ОУ Гц

Отсюда следует, что вероятность по крайней мере одного возвращения в состояние Ej задается формулой

Следовательно, система обязательно вернется в состояние j, если /. = 1 . Обозначив через среднее время возвращения, получаем

jj=t<]-

Если fu < 1, то неизвестно, вернется ли система в состояние Et , и, следовательно, Ц=оо.

Исходя из определения первого времени возвращения, состояния марковской цепи можно классифицировать следующим образом.

1. Состояние является невозвратным, если у\ < 1, т.е. ц;> =<х>.

2. Состояние является возвратным, если fM= \.

3. Возвратное состояние является нулевым, если ци= оо, и ненулевым, когда

< оо (т.е. конечно).

4. Состояние называется периодическим с периодом t, если возвращение в него возможно только через число шагов, кратное t: t, 2t, 3t, ... Это означает, что

если п не делится на t без остатка, то pf = 0 .

5. Возвратное состояние является эргодическим, если оно ненулевое и апериодическое.

Если все состояния цепи Маркова являются эргодическими, то цепь неприводи-ма. В этом случае распределение абсолютных вероятностей состояний

аН=а(о)р

всегда однозначно сходится к предельному распределению при п - оо, где предель-

и (о)

ное распределение не зависит от начальных вероятностей лу. Справедлива следующая теорема.

Теорема 19.5.1. Все состояния в неприводимой бесконечной цепи Маркова могут принадлежать к одному и только одному из следующих трех классов: невоз-

вратных, возвратных нулевых или возвратных ненулевых состояний. Во всех случаях все состояния являются сообщающимися и имеют один и тот же период. В частном случае, когда в цепи конечное число состояний, она не может содержать только невозвратные или какие-либо нулевые состояния.

Предельные распределения в неприводимых цепях Маркова. Из примера 19.5.1 видно, что с ростом числа переходов абсолютная вероятность состояний становится независимой от начального распределения. В данном разделе описывается метод вычисления предельного распределения вероятностей состояний в неприводимой цепи. Мы ограничимся рассмотрением только апериодических состояний, так как это единственный класс состояний, используемый в дальнейшем. Кроме того, анализ периодических состояний является довольно сложным.

Существование предельного распределения в неприводимой апериодической цепи зависит от класса ее состояний. Таким образом, рассматривая три класса состояний, указанных в теореме 19.5.1, можно сформулировать следующую теорему.

Теорема 19.5.2. Если в неприводимой апериодической цепи Маркова

а) все состояния невозвратные или нулевые, то рп) -> 0 при п->оо для всех i и j и предельного распределения не существует,

б) все состояния эргодические, то

lima = я у = 0, 1, 2, ....

где nj - предельное (установившееся) распределение. Вероятности nj определяются однозначно и не зависят от я}0. Величины /гу можно определить из системы уравнении

Среднее время возвращения в состояние j при этом определяется формулой

Пример 19.5.3

Рассмотрим задачу из примера 19.5.1. Для определения установившегося распределения вероятностей используем соотношения

я, =0,2;!, +0,6ti2, 7i2 =0,871, +0,4ti2,

7t, + 7t2 = 1.

1 Заметим, что одно из уравнений nt = jt,p является избыточным.