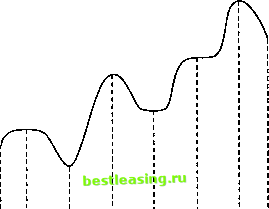а хх х2 хг х4 х5 х6 b х

Рас. 20.1. Экстремумы функции одной переменной

Заметим, что хотя точка х1 является точкой максимума функции f(x) (рис. 20.1), она отличается от остальных локальных максимумов f(x) тем, что по крайней мере в одной точке ее окрестности значение функции f(x) совпадает с f(x,). Точка х, по этой причине называется нестрогим (слабым) максимумом функции f(x), в отличие, например, от точки х3, которая является строгим максимумом f(x). Нестрогий максимум, следовательно, подразумевает наличие (бесконечного количества) различных точек, которым соответствует одно и то же максимальное значение функции. Аналогичные результаты имеют место в точке xt, где функция f(x) имеет нестрогий минимум. В общем случае Х0 является точкой нестрогого максимума функции f(x), если /(Х0 + h) < /(Х0), и точкой ее строгого максимума, если /(Х0 + h) < /(Х0), где h - вектор, определенный выше.

На рис. 20.1 легко заметить, что первая производная функции / (тангенс угла наклона касательной к графику функции) равна 0 во всех ее экстремальных точках. Однако это условие выполняется и в точках перегиба и седловых точках функции /, таких как точка хь. Если точка, в которой угол наклона касательной к графику функции (градиент функции) равен нулю, не является в то же время точкой экстремума (максимума или минимума), то она автоматически должна быть точкой перегиба или седловой точкой.

20.1.1. Необходимые и достаточные условия существования экстремума

В этом разделе излагаются необходимые и достаточные условия существования экстремумов функции п переменных /(X). При этом предполагается, что первые и вторые частные производные функции f(X) непрерывны в каждой точке X.

Теорема 20.1.1. Необходимым условием того, что точка Х0 является экстремальной точкой функции /(X), служит равенство

V/(X0) = 0.

Доказательство. Из теоремы Тейлора следует, что при 0 < в< 1 имеет место разложение функции f(X)

/(Х + h) -/(Х0) = V/(X0)h + ib/Hh Xi+0h,

где h - вектор, определенный выше. Для достаточно малых значений остаточный член yhrHh является величиной порядка А2 . Следовательно,

/(X0 + h)-/(X0) = V/(X0)h + O(A2) = V/(X0)h.

Пусть Х0 - точка минимума функции /(X). Докажем от противного, что градиент V/(X0) функции /(X) в точке минимума Х0 равен нулю. Пусть это условие не выполняется; тогда для некоторого j должно выполняться условие

Шй<0 или *Ш>й

дх} dXj

Знак Лу всегда можно выбрать таким образом, чтобы

Полагая остальные Л; равными нулю, из разложения Тейлора получаем неравенство

X0 + h)</(X0).

Этот результат противоречит предположению, что Х0 - точка минимума. Следовательно, величина V/(X0) должна равняться нулю. Доказательство для точки максимума проводится аналогично.

Так как необходимое условие выполняется также в точках перегиба и седловых точках, точки, удовлетворяющие уравнению V/(X0) = 0, называют стационарными. Следующая теорема устанавливает достаточные условия того, что стационарная точка Х0 является экстремальной.

Теорема 20.1.2. Для того чтобы стационарная точка Х0 была экстремальной, достаточно, чтобы матрица Гессе Н в точке Х0 была

а) положительно определенной (тогда Х0 - точка минимума);

б) отрицательно определенной (тогда Х0 - точка максимума).

Доказательство. Согласно теореме Тейлора при 0 < в< 1 имеем

/(х0 + ь) - /(х.) = v/(x,)h +UTm .

Поскольку Х0 - стационарная точка, по теореме 20.1.1 V/(X0) = 0. Таким образом,

/(X0 + h)-/(X0) = ihrHh0b. Если Х0 - точка минимума, то

7-(X0 + h)>/(X0)

для всех ненулевых векторов h. Следовательно, в точке минимума Х0 должно выполняться неравенство

ihrHhXi.oh>0.

Непрерывность вторых частных производных функции /(X) гарантирует, что величина ihrHh имеет один и тот же знак как в точке Х0, так и X0+tfli. Так как hrHh представляет собой квадратичную форму (см. раздел А.3), ее значение (и, следова-

тельно, hrHh xoh) положительно тогда и только тогда, когда HXi -положительно определенная матрица. Это означает, что положительная определенность матрицы Гессе в стационарной точке Х0 является достаточным условием существования в этой точке минимума. Путем аналогичных рассуждений доказывается, что стационарная точка является точкой максимума, если матрица Гессе в этой точке отрицательно определена.

Пример 20.1.1

Рассмотрим функцию

/(х х2,х,) = .V, + 2хъ + лг,дг3 -х2 -х\ -х\. Необходимое условие экстремума Vfi\) = 0 здесь принимает следующий вид.

= 1-2*. =0,

- = х,-2хг =0, дх2

- = 2 + х2-2х,=0. ох,

Решением этой системы уравнений является точка Х0 = (1/2, 2/3, 4/3). Для проверки выполнения условия достаточности вычислим

-2 1 1 -2

Угловые миноры матрицы Н х равны -2, 4 и -6 соответственно. В этом случае Н Xi

является отрицательно определенной матрицей (см. раздел А.З), откуда следует, что точка Х0 = (1/2, 2/3, 4/3) является точкой максимума.

В общем случае, когда матрица Н х является неопределенной, точка Х0 должна быть седловой. Если же матрица Н х оказывается полуопределенной, то соответствующая точка Х0 может как быть, так и не быть экстремальной. При этом формулировка достаточного условия существования экстремума значительно усложняется, ибо для этого необходимо учитывать члены более высоких порядков в разложении Тейлора.

Применим достаточные условия, полученные в теореме 20.1.2, к функции одной переменной. Пусть у0 - стационарная точка функции тогда